题目内容
15.解不等式$\frac{1}{2}$x-$\frac{2}{3}$≥$\frac{2}{3}$x-$\frac{1}{3}$,并把它的解集在数轴上表示出来.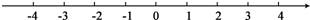
分析 先去分母、移项得到3x-4x≥-2+4,然后合并后把x的系数化为1即可得到不等式的解集,再利用数轴表示解集.
解答 解:去分母得3x-4≥4x-2,
移项得3x-4x≥-2+4,
合并得-x≥2,
系数化为1得x≤-2,
用数轴表示为: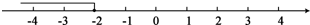 .
.
点评 本题考查了解一元一次不等式:解一元一次不等式的一般步骤为:先去括号,再移项,接着合并同类项,然后把系数化为1.也考查了在数轴上表示不等式的解集.

练习册系列答案
相关题目
6. 如图,正六边形ABCDEF内接于⊙O,已知弦心距OM=3,则此正六边形的边长为( )
如图,正六边形ABCDEF内接于⊙O,已知弦心距OM=3,则此正六边形的边长为( )
 如图,正六边形ABCDEF内接于⊙O,已知弦心距OM=3,则此正六边形的边长为( )
如图,正六边形ABCDEF内接于⊙O,已知弦心距OM=3,则此正六边形的边长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
10.在下面的四个几何体中,它们各自的左视图与主视图不相同的是( )
| A. |  正方体 | B. | 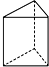 三棱柱 | C. | 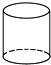 圆柱 | D. | 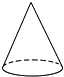 圆锥 |
7.若二次根式$\sqrt{x-2}$有意义,则x的取值范围是( )
| A. | x≤0 | B. | x≥0 | C. | x≤2 | D. | x≥2 |