题目内容
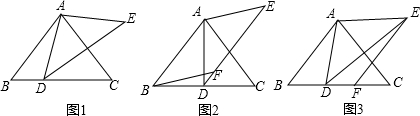
4.如图1,在△ABC中,AB=AC,∠ABC=α,D是BC边上一点,以AD为边作△ADE,使AE=AD,∠DAE+∠BAC=180°.(1)直接写出∠ADE的度数(用含α的式子表示);
(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.
分析 (1)由在△ABC中,AB=AC,∠ABC=α,可求得∠BAC=180°-2α,又由AE=AD,∠DAE+∠BAC=180°,可求得∠DAE=2α,继而求得∠ADE的度数;
(2)①由四边形ABFE是平行四边形,易得∠EDC=∠ABC=α,则可得∠ADC=∠ADE+∠EDC=90°,证得AD⊥BC,又由AB=AC,根据三线合一的性质,即可证得结论;
②由在△ABC中,AB=AC,∠ABC=α,可得∠B=∠C=α,四边形ABFE是平行四边形,可得AE∥BF,AE=BF.即可证得:∠EAC=∠C=α,又由(1)可证得AD=CD,又由AD=AE=BF,证得结论.
解答 解:(1)∵在△ABC中,AB=AC,∠ABC=α,
∴∠BAC=180°-2α,
∵∠DAE+∠BAC=180°,
∴∠DAE=2α,
∵AE=AD,
∴∠ADE=90°-α;
(2)①证明:∵四边形ABFE是平行四边形,
∴AB∥EF.
∴∠EDC=∠ABC=α,
由(1)知,∠ADE=90°-α,
∴∠ADC=∠ADE+∠EDC=90°,
∴AD⊥BC.
∵AB=AC,
∴BD=CD;
②证明:∵AB=AC,∠ABC=α,
∴∠C=∠B=α.
∵四边形ABFE是平行四边形,
∴AE∥BF,AE=BF.
∴∠EAC=∠C=α,
由(1)知,∠DAE=2α,
∴∠DAC=α,
∴∠DAC=∠C.
∴AD=CD.
∵AD=AE=BF,
∴BF=CD.
∴BD=CF.
点评 此题考查了平行四边形的判定与性质以及等腰三角形的性质与判定.注意(2)①中证得AD⊥BC是关键,(2)②中证得AD=CD是关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
14.梯形ABCD中,AD∥BC,若要使顺次连接ABCD各边中点所得的四边形为矩形,只需( )
| A. | AB=DC | B. | AC=BD | C. | AB=DC且AC=BD | D. | AC⊥BD |
12.小明家端午节聚会,需要12个粽子.小明发现某商场正好推出粽子“买10赠1”的促销活动,即顾客每买够10个粽子就送1个粽子.已知粽子单价是5元/个,按此促销方法,小明至少应付钱( )
| A. | 45元 | B. | 50元 | C. | 55元 | D. | 60元 |
9.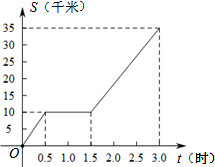 一辆自行车在公路上行驶,中途发生了故障,停下修理一段时间后继续前进.已知行驶路程S(千米)与所用时间t(时)的函数关系的图象如图所示,那么自行车发生故障后继续前进的速度为( )
一辆自行车在公路上行驶,中途发生了故障,停下修理一段时间后继续前进.已知行驶路程S(千米)与所用时间t(时)的函数关系的图象如图所示,那么自行车发生故障后继续前进的速度为( )
 一辆自行车在公路上行驶,中途发生了故障,停下修理一段时间后继续前进.已知行驶路程S(千米)与所用时间t(时)的函数关系的图象如图所示,那么自行车发生故障后继续前进的速度为( )
一辆自行车在公路上行驶,中途发生了故障,停下修理一段时间后继续前进.已知行驶路程S(千米)与所用时间t(时)的函数关系的图象如图所示,那么自行车发生故障后继续前进的速度为( )| A. | 20千米/时 | B. | $\frac{35}{3}$千米/时 | C. | 10千米/时 | D. | $\frac{50}{3}$千米/时 |
13.2015年春节,顺义区相关部门做了充分的准备工作,确保了消费品市场货源充足.据统计,春节一周长假期间共实现销售收入约3.284亿元,同比增长4.8%.将“3.284亿”用科学记数法表示正确的是( )
| A. | 3.284×108 | B. | 32.84×107 | C. | 3.284×107 | D. | 3.284×109 |
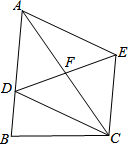 如图,在△ABC中,D为AB边上一点,F为AC的中点,连接DF并延长至E,使得EF=DF,连接AE和EC.
如图,在△ABC中,D为AB边上一点,F为AC的中点,连接DF并延长至E,使得EF=DF,连接AE和EC.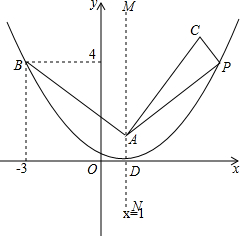 如图,在直角坐标系中,已知点A(1,1)、B(-3,4);将线段BA绕点A顺时针旋转90°得到AC;顶点为D(1,0)抛物线过点B.
如图,在直角坐标系中,已知点A(1,1)、B(-3,4);将线段BA绕点A顺时针旋转90°得到AC;顶点为D(1,0)抛物线过点B.