��Ŀ����
10�� ��ͼ��������y=$\frac{1}{4}$x2+bx+c��x�ύ�ڵ�A��-2��0������y���ڵ�B��0��-$\frac{5}{2}$����ֱ��y=kx+$\frac{3}{2}$����A��y�ύ�ڵ�C���������ߵ���һ������ΪD��
��ͼ��������y=$\frac{1}{4}$x2+bx+c��x�ύ�ڵ�A��-2��0������y���ڵ�B��0��-$\frac{5}{2}$����ֱ��y=kx+$\frac{3}{2}$����A��y�ύ�ڵ�C���������ߵ���һ������ΪD����1����գ�b=-$\frac{3}{4}$��c=-$\frac{5}{2}$��k=$\frac{3}{4}$��
��2�����P��ֱ��AD�·�����������һ���㣨��ͬ��A��D���㣩������P��y���ƽ���ߣ���ֱ��AD�ڵ�M����DE��y���ڵ�E��̽�����Ƿ���������ĵ�P��ʹ�ı���PMEC��ƽ���ı��Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��3���ڣ�2���������£���PN��AD�����PMN���ܳ�Ϊl����P�ĺ�����Ϊx����l��x�ĺ�����ϵʽ�������l�����ֵ��
���� ��1�����ô���ϵ�������ɽ�����⣻
��2����P�������ǣ�x��$\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$������M�������ǣ�x��$\frac{3}{4}$x+$\frac{3}{2}$������PM=�� $\frac{3}{4}$x+$\frac{3}{2}$��-�� $\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$��=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4����EC=PM�õ�-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=6���ⷽ�̼��ɣ�
��3��ͨ�����������Ρ�PMN�ס�CDE��������֪���� $\frac{��PMN���ܳ�}{��CEE���ܳ�}$=$\frac{PM}{DC}$ �������κ������ɽ�����⣮
��� �⣺��1����y=$\frac{1}{4}$x2+bx+c������A��-2��0����B��0��-$\frac{5}{2}$��
���ɴ˵� $\left\{\begin{array}{l}{1-2b+c=0}\\{c=-\frac{5}{2}}\end{array}\right.$�����$\left\{\begin{array}{l}{b=-\frac{3}{4}}\\{c=-\frac{5}{2}}\end{array}\right.$��
�������ߵĽ���ʽ��y=$\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$��
��ֱ��y=kx+$\frac{3}{2}$������A��-2��0��
��-2k+$\frac{3}{2}$=0��
��ã�k=$\frac{3}{4}$��
��ֱ�ߵĽ���ʽ�� y=$\frac{3}{4}$x+$\frac{3}{2}$��
�ʴ�Ϊ-$\frac{3}{4}$��-$\frac{5}{2}$��$\frac{3}{4}$��
��2������D�������ǣ�8��7 $\frac{1}{2}$������C�������ǣ�0��$\frac{3}{2}$����
��CE=6��
��P�������ǣ�x��$\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$������M�������ǣ�x��$\frac{3}{4}$x+$\frac{3}{2}$��
��Ϊ��P��ֱ��AD���·���
��ʱPM=�� $\frac{3}{4}$x+$\frac{3}{2}$��-�� $\frac{1}{4}$x2-$\frac{3}{4}$x-$\frac{5}{2}$��=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��
����PM��y�ᣬҪʹ�ı���PMEC��ƽ���ı��Σ�����PM=CE��
��-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=6
��������̵ã�x1=2��x2=4��
��x=2ʱ��y=-3��
��x=4ʱ��y=-$\frac{3}{2}$��
��ˣ�ֱ��AD�·����������ϴ��������ĵ�P��ʹ�ı���PMEC��ƽ���ı��Σ�
��P�������ǣ�2��-3���ͣ�4��-$\frac{3}{2}$����
��3����Rt��CDE�У�DE=8��CE=6 �ɹ��ɶ����ã�DC=$\sqrt{{8}^{2}+{6}^{2}}$=10
���CDE���ܳ���24��
��PM��y�ᣬ���PMN=��DCE��
�ߡ�PNM=��DEC=90�㣬���PMN�ס�CDE��
��$\frac{��PMN���ܳ�}{��CDE���ܳ�}$=$\frac{PM}{DC}$���� $\frac{m}{24}$=$\frac{-\frac{1}{4}{x}^{2}+\frac{3}{2}x+4}{10}$��
���������ã�m��x�ĺ�����ϵʽ�ǣ�m=-$\frac{3}{5}$x2+$\frac{18}{5}$x+$\frac{48}{5}$��
m=-$\frac{3}{5}$ ��x-3��2+15��
��-$\frac{3}{5}$��0��
��m�����ֵ����x=3ʱ��m�����ֵ��15��
���� ���⿼���˶��κ����ۺ��⡢һ�κ�����Ӧ�á�����ϵ������ƽ���ı��ε����ʡ����������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�ṹ�����κ��������ֵ���⣬ѧ���÷��̵�˼��˼�����⣬�����п�ѹ���⣮

 ��ͼ����?ABCD�У�AB=2��BC=4����D=60�㣬��P��Q�ֱ���AC��BC�ϵĶ��㣬�ڵ�P�͵�Q�˶��Ĺ����У�PB+PQ����СֵΪ��������
��ͼ����?ABCD�У�AB=2��BC=4����D=60�㣬��P��Q�ֱ���AC��BC�ϵĶ��㣬�ڵ�P�͵�Q�˶��Ĺ����У�PB+PQ����СֵΪ��������| A�� | 4 | B�� | 3 | C�� | 2$\sqrt{3}$ | D�� | 4$\sqrt{3}$ |
| A�� | ��ȵĽ��ǶԶ��� | B�� | ͬλ����� | ||
| C�� | ��ֱ��ƽ�У�ͬ���ڽ���� | D�� | ���߶���� |
 ��1������x+1��2-x��2-x��
��1������x+1��2-x��2-x�� С�Ժ�С����������еĻ��С��˵��������һ�����������һ�����ڣ���7���������֮����84�죬��֪�����Ǽ��ų�ȥ��ô����С��˵�������ȥ�˾˼�ס��7�죬�������ټ��·���Ҳ��84�����ܲ³����Ǽ��¼��Żصļң����Կ��г����̣����С�ԡ�С�������⣮����ʾ��7��1��-9��1����٣�
С�Ժ�С����������еĻ��С��˵��������һ�����������һ�����ڣ���7���������֮����84�죬��֪�����Ǽ��ų�ȥ��ô����С��˵�������ȥ�˾˼�ס��7�죬�������ټ��·���Ҳ��84�����ܲ³����Ǽ��¼��Żصļң����Կ��г����̣����С�ԡ�С�������⣮����ʾ��7��1��-9��1����٣�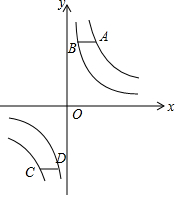 ��ͼ����֪��A��C�ڷ���������y=$\frac{4}{x}$��ͼ���ϣ���B��D�ڷ���������y=$\frac{b}{x}$��0��b��4����ͼ���ϣ�AB��CD��x�ᣬAB��CD��x������࣬A��C��������ֱ�Ϊm��m��0����n��n��0����
��ͼ����֪��A��C�ڷ���������y=$\frac{4}{x}$��ͼ���ϣ���B��D�ڷ���������y=$\frac{b}{x}$��0��b��4����ͼ���ϣ�AB��CD��x�ᣬAB��CD��x������࣬A��C��������ֱ�Ϊm��m��0����n��n��0����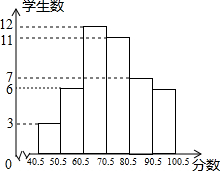 ij��ѧ���μӻ���֪ʶ��������֪�����÷ֶ����������Ѳ���ѧ���ijɼ��������Ϊ6С�飬���������ɼ���Ƶ���ֲ�ֱ��ͼ����ͼ��ʾ��������ͼ�е���Ϣ���ɵóɼ�����60�ֵ�ѧ��ռȫ����������İٷ�����80%��
ij��ѧ���μӻ���֪ʶ��������֪�����÷ֶ����������Ѳ���ѧ���ijɼ��������Ϊ6С�飬���������ɼ���Ƶ���ֲ�ֱ��ͼ����ͼ��ʾ��������ͼ�е���Ϣ���ɵóɼ�����60�ֵ�ѧ��ռȫ����������İٷ�����80%��