题目内容
2.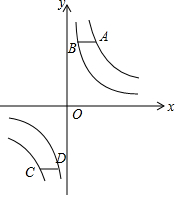 如图,已知点A、C在反比例函数y=$\frac{4}{x}$的图象上,点B、D在反比例函数y=$\frac{b}{x}$(0<b<4)的图象上,AB∥CD∥x轴,AB、CD在x轴的两侧,A、C的纵坐标分别为m(m>0)、n(n<0).
如图,已知点A、C在反比例函数y=$\frac{4}{x}$的图象上,点B、D在反比例函数y=$\frac{b}{x}$(0<b<4)的图象上,AB∥CD∥x轴,AB、CD在x轴的两侧,A、C的纵坐标分别为m(m>0)、n(n<0).(1)若m+n=0,求证:四边形ABCD为平行四边形;
(2)若AB=$\frac{3}{4}$,CD=$\frac{3}{2}$,m-n=6,求b的值.
分析 (1)由题意可知:A$(\frac{4}{m},m)$,B$(\frac{b}{m},m)$,C$(\frac{4}{n},n)$,D$(\frac{b}{n},n)$,从而可证明CD=$\frac{b-4}{-m}=\frac{-(4-b)}{-m}=\frac{4-b}{m}=AB$,由于AB∥CD,所以四边形ABCD是平行四边形.
(2)由于AB=$\frac{3}{4}$,CD=$\frac{3}{2}$,m-n=6,所以列出关于m、n、b的方程组,从而求出b的值.
解答 解:(1)∵AB∥CD∥x轴,AB、CD在x轴的两侧,A、C的纵坐标分别为m、n其中m>0,n<0,
∴A$(\frac{4}{m},m)$,B$(\frac{b}{m},m)$,C$(\frac{4}{n},n)$,D$(\frac{b}{n},n)$
∴AB=$\frac{4-b}{m}$,CD=$\frac{b-4}{n}$
∵m+n=0,
∴CD=$\frac{b-4}{-m}=\frac{-(4-b)}{-m}=\frac{4-b}{m}=AB$,
又∵AB∥CD
∴四边形ABCD为平行四边形
(2)∵AB=$\frac{3}{4}$,CD=$\frac{3}{2}$,m-n=6,
∴$\left\{\begin{array}{l}\frac{4-b}{m}=\frac{3}{4}\\ \frac{b-4}{n}=\frac{3}{2}\\ m-n=6\end{array}\right.$
解得:b=1,
∴b的值为1
点评 本题考查反比例函数的综合问题,解题的关键是正确理解点在反比例函数图象上的意义,本题属于中等题型.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
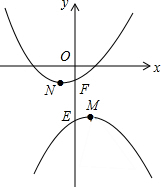 如图,抛物线y1=-ax2+2ax-a-3(a>0)和y2=a(x+1)2-1(a>0)的顶点分别为M、N,与y轴分别交于E、F.
如图,抛物线y1=-ax2+2ax-a-3(a>0)和y2=a(x+1)2-1(a>0)的顶点分别为M、N,与y轴分别交于E、F. 如图,抛物线y=$\frac{1}{4}$x2+bx+c与x轴交于点A(-2,0),交y轴于点B(0,-$\frac{5}{2}$),直线y=kx+$\frac{3}{2}$过点A与y轴交于点C,与抛物线的另一个交点为D.
如图,抛物线y=$\frac{1}{4}$x2+bx+c与x轴交于点A(-2,0),交y轴于点B(0,-$\frac{5}{2}$),直线y=kx+$\frac{3}{2}$过点A与y轴交于点C,与抛物线的另一个交点为D.
 将下列各选项中的平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )
将下列各选项中的平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )



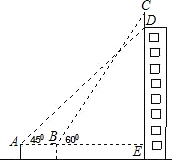 如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数)
如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数)