题目内容
2.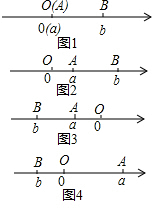 阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1所示,|AB|=|OB|=|b|=|a-b|;当A、B两点都不在原点时.
阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1所示,|AB|=|OB|=|b|=|a-b|;当A、B两点都不在原点时.(1)如图2所示,点A、B都在原点右边,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
(2)如图3所示,点A、B都在原点左边,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
(3)如图4所示,点A、B在原点两边,|AB|=|OB|+|OA|=|b|+|a|=a+(-b)=|a-b|.
综上所述,数轴上A、B两点之间的距离表示为|AB|=|a-b|.
根据阅读材料回答下列问题:
(1)数轴上表示-2和-5的两点之间的距离是3,数轴上表示1和-3的两点之间的距离是4;
(2)数轴上表示x和-3的两点A、B之间的距离是|x+3|,如果|AB|=2,则x为-1或5.
(3)当代数式|x+1|+|x-2|取最小值时,即在数轴上,表示x的动点到表示-1和2的两个点之间的距离和最小,这个最小值为3.相应的x的取值范围是-1≤x≤2.
分析 根据数轴上A、B两点之间的距离表示为|AB|=|a-b|即可求出答案.
解答 解:(1)-2-(-5)=3,
1-(-3)=4,;
(2)|x-(-3)|=|x+3|,
∵|x+3|=2,
∴x+3=±2,
∴x=-1或5;
(3)由题意可知:当x在-1与2之间时,
此时,代数式|x+1|+|x-2|取最小值,
最小值为2-(-1)=3,
此时x的取值范围为:-1≤x≤2;
故答案为:(1)3,4; (2)|x+3|,-1或-5;(3)3,-1≤x≤2.
点评 本题考查绝对值的意义,涉及有理数的运算,整式化简,绝对值的性质.

练习册系列答案
相关题目
13.下列函数关系式中,y不是x的函数的是( )
| A. | y=-x | B. | |y|=2x | C. | y=|2x| | D. | y=2x2+4 |
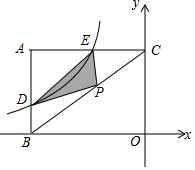 如图,在平面直角坐标系中,矩形OCAB的两边在直角坐标系的坐标轴上,顶点A在第二象限,OB=4,OC=3,点D是边AB上的一个动点(点D不与A,B重合),过点D的反比例函数y=$\frac{m}{x}$的图象与边AC交于点E.
如图,在平面直角坐标系中,矩形OCAB的两边在直角坐标系的坐标轴上,顶点A在第二象限,OB=4,OC=3,点D是边AB上的一个动点(点D不与A,B重合),过点D的反比例函数y=$\frac{m}{x}$的图象与边AC交于点E.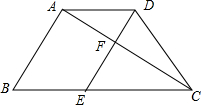 如图,已知梯形ABCD中,AD∥BC,AB=4,AD=3,AB⊥AC,AC平分∠DCB,过点DE∥AB,分别交AC、BC于F、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.求:
如图,已知梯形ABCD中,AD∥BC,AB=4,AD=3,AB⊥AC,AC平分∠DCB,过点DE∥AB,分别交AC、BC于F、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.求: 如图,为了拧开一个边长为a的正六边形六角形螺帽,扳手张开b=30mm时正好把螺帽嵌进,则螺帽的边长a最大为10$\sqrt{3}$mm.
如图,为了拧开一个边长为a的正六边形六角形螺帽,扳手张开b=30mm时正好把螺帽嵌进,则螺帽的边长a最大为10$\sqrt{3}$mm.