题目内容
11. 如图,为了拧开一个边长为a的正六边形六角形螺帽,扳手张开b=30mm时正好把螺帽嵌进,则螺帽的边长a最大为10$\sqrt{3}$mm.
如图,为了拧开一个边长为a的正六边形六角形螺帽,扳手张开b=30mm时正好把螺帽嵌进,则螺帽的边长a最大为10$\sqrt{3}$mm.
分析 根据题意,即是求该正六边形的边心距的2倍.构造一个由半径、半边、边心距组成的直角三角形,且其半边所对的角是30度,再根据锐角三角函数的知识求解.
解答 解:设正多边形的中心是O,其一边是AB,
∴∠AOB=∠BOC=60°,
∴OA=OB=AB=OC=BC,
∴四边形ABCO是菱形,
∵AB=a,∠AOB=60°,
∴cos∠BAC=$\frac{AM}{AB}$,
∵OA=OC,且∠AOB=∠BOC,
∴AM=MC=$\frac{1}{2}$AC,
∵AC=30mm,
∴a=AB=$\frac{AM}{cos30°}$=$\frac{15}{\frac{\sqrt{3}}{2}}$=10$\sqrt{3}$(mm).
故答案为:10$\sqrt{3}$.
点评 本题考查了正多边形和圆的知识,构造一个由半径、半边、边心距组成的直角三角形,熟练运用锐角三角函数进行求解

练习册系列答案
相关题目
19.圆锥体的底面半径为2,全面积为12π,则其侧面展开图的圆心角为( )
| A. | 90° | B. | 120° | C. | 150° | D. | 180° |
6.下列计算正确的是( )
| A. | (am)n=am+n | B. | 2a+a=3a2 | C. | (a2b)3=a6b3 | D. | a2•a3=a6 |
16.下列计算正确的是( )
| A. | 5a+2a=7a2 | B. | 5a-2a=3 | C. | 5a-2a=3a | D. | -ab+2ab2=ab2 |
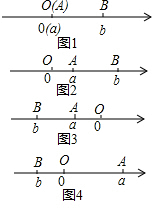 阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1所示,|AB|=|OB|=|b|=|a-b|;当A、B两点都不在原点时.
阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1所示,|AB|=|OB|=|b|=|a-b|;当A、B两点都不在原点时.