题目内容
14.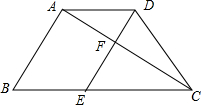 如图,已知梯形ABCD中,AD∥BC,AB=4,AD=3,AB⊥AC,AC平分∠DCB,过点DE∥AB,分别交AC、BC于F、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.求:
如图,已知梯形ABCD中,AD∥BC,AB=4,AD=3,AB⊥AC,AC平分∠DCB,过点DE∥AB,分别交AC、BC于F、E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.求:(1)向量$\overrightarrow{DC}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示);
(2)tanB的值.
分析 (1)首先证明四边形ABED是平行四边形,推出DE=AB,推出$\overrightarrow{DE}$=$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{EC}$=$\frac{1}{2}$$\overrightarrow{BC}$=$\frac{1}{2}$$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$.
(2)由△DFC∽△BAC,推出$\frac{DC}{BC}$=$\frac{CF}{CA}$=$\frac{1}{2}$,求出BC,在Rt△BAC中,∠BAC=90°,根据AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$,由tanB=$\frac{AC}{BC}$,即可解决问题.
解答 解:∵AD∥BC,
∴∠DAC=∠ACB,
∴AC平分∠DCB,
∴∠DCA=∠ACB,
∴∠DAC=∠DCA,
∴AD=DC,
∵DE∥AB,AB⊥AC,
∴DE⊥AC,
∴AF=CF,
∴BE=CE,
∵AD∥BC,DE∥AB,
∴四边形ABED是平行四边形,
∴DE=AB,
∴$\overrightarrow{DE}$=$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{EC}$=$\frac{1}{2}$$\overrightarrow{BC}$=$\frac{1}{2}$$\overrightarrow{b}$,
∴$\overrightarrow{DC}$=$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$.
(2)∵∠DCF=∠ACB,∠DFC=∠BAC=90°,
∴△DFC∽△BAC,
∴$\frac{DC}{BC}$=$\frac{CF}{CA}$=$\frac{1}{2}$,
∵CD=AD=3,∴BC=6,
在Rt△BAC中,∠BAC=90°,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$,
∴tanB=$\frac{AC}{BC}$=$\frac{2\sqrt{5}}{4}$=$\frac{\sqrt{5}}{2}$.
点评 本题考查平面向量、梯形、解直角三角形、平行四边形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识,属于基础题.

| A. | 90° | B. | 120° | C. | 150° | D. | 180° |
| A. | (am)n=am+n | B. | 2a+a=3a2 | C. | (a2b)3=a6b3 | D. | a2•a3=a6 |
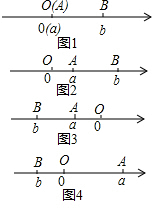 阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1所示,|AB|=|OB|=|b|=|a-b|;当A、B两点都不在原点时.
阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1所示,|AB|=|OB|=|b|=|a-b|;当A、B两点都不在原点时. 能展开成如图所示的几何体名称是三棱柱.
能展开成如图所示的几何体名称是三棱柱.