题目内容
 如图,半圆O的半径为1,AC⊥AB,BD⊥AB,且AC=1,BD=3,P是半圆上任意一点,则封闭图形ABDPC面积的最大值是
如图,半圆O的半径为1,AC⊥AB,BD⊥AB,且AC=1,BD=3,P是半圆上任意一点,则封闭图形ABDPC面积的最大值是考点:面积及等积变换
专题:
分析:连接DC,并延长交BA的延长线于点G,欲使封闭图形ACPDB的面积最大,因梯形ACDB的面积为定值,故只需△CPD的面积最小.而CD为定值,故只需使动点P到CD的距离最小.为此作半圆平行于CD的切线EF,设切点为P′,并分别交BD及BA的延长线于点F,E.连接OC,由△CGA∽△DGB即可求出GA=AO=AC=1,再根据当动点P取在P′的位置时,到CD的距离最小,进而可求出答案.
解答: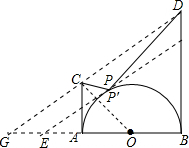 解:如图,连接DC,并延长交BA的延长线于点G,欲使封闭图形ACPDB的面积最大,
解:如图,连接DC,并延长交BA的延长线于点G,欲使封闭图形ACPDB的面积最大,
因梯形ACDB的面积为定值,故只需△CPD的面积最小.
而CD为定值,故只需使动点P到CD的距离最小.
为此作半圆平行于CD的切线EF,设切点为P′,并分别交BD及BA的延长线于点F,E.
连接OC,
∵CA⊥AB,DB⊥AB,
∴△CGA∽△DGB,
∴
=
,
∴GA=AO=AC=1.
∴△ACO和△GAC是等腰直角三角形,
∴∠GCA=∠OCA=45°,
∴∠GCO=90°,
∴OC⊥GD.OC⊥EF,
∴切点P′就是OC与半圆的交点.
即当动点P取在P′的位置时,到CD的距离最小,而OC=
,
∴CP?=
-1,
∴S△CP?D=
×2
×(
-1)=2-
,
∴封闭图形ACPDB的最大面积为:
×(1+3)×2-(2-
)=4-2+
=2+
.
故答案为:2+
.
 解:如图,连接DC,并延长交BA的延长线于点G,欲使封闭图形ACPDB的面积最大,
解:如图,连接DC,并延长交BA的延长线于点G,欲使封闭图形ACPDB的面积最大,因梯形ACDB的面积为定值,故只需△CPD的面积最小.
而CD为定值,故只需使动点P到CD的距离最小.
为此作半圆平行于CD的切线EF,设切点为P′,并分别交BD及BA的延长线于点F,E.
连接OC,
∵CA⊥AB,DB⊥AB,
∴△CGA∽△DGB,
∴
| CA |
| DB |
| GA |
| GB |
∴GA=AO=AC=1.
∴△ACO和△GAC是等腰直角三角形,
∴∠GCA=∠OCA=45°,
∴∠GCO=90°,
∴OC⊥GD.OC⊥EF,
∴切点P′就是OC与半圆的交点.
即当动点P取在P′的位置时,到CD的距离最小,而OC=
| 2 |
∴CP?=
| 2 |
∴S△CP?D=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
∴封闭图形ACPDB的最大面积为:
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
故答案为:2+
| 2 |
点评:本题考查的是面积及等积变换,解答此题的关键是作出辅助线,构造出相似三角形,利用相似三角形的性质解答.

练习册系列答案
相关题目
若x=
+
,y=
-
,则
=( )
| a |
| b |
| a |
| b |
| 1 |
| xy |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知x+
=7(0<x<1),则
-
的值为( )
| 1 |
| x |
| x |
| 1 | ||
|
A、-
| ||
B、-
| ||
C、
| ||
D、
|
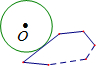 如图,⊙O沿凸n边形的外侧(圆和边相切)无滑动地滚动一周回到原来的位置,当⊙O和凸n边形的周长相等时,那么⊙O自身转动了( )圈.
如图,⊙O沿凸n边形的外侧(圆和边相切)无滑动地滚动一周回到原来的位置,当⊙O和凸n边形的周长相等时,那么⊙O自身转动了( )圈. 如图,在△ABC中,AP=QP=QB=BC,AB=AC.求∠A的度数.
如图,在△ABC中,AP=QP=QB=BC,AB=AC.求∠A的度数.