题目内容
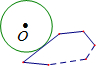 如图,⊙O沿凸n边形的外侧(圆和边相切)无滑动地滚动一周回到原来的位置,当⊙O和凸n边形的周长相等时,那么⊙O自身转动了( )圈.
如图,⊙O沿凸n边形的外侧(圆和边相切)无滑动地滚动一周回到原来的位置,当⊙O和凸n边形的周长相等时,那么⊙O自身转动了( )圈.| A、1 | B、2 | C、3 | D、4 |
考点:直线与圆的位置关系
专题:计算题
分析:根据圆的运动方式不同分两种情况考虑:(i)当圆沿着线段的一个端点无滑动地滚动到另一个端点时,根据圆自身转动的圈数=线段的长度÷圆的周长,由⊙O和凸n边形的周长相等,可得出⊙O自身恰好转动了一圈;(ii)当⊙O在某边的一端,滚动经过该端点(即顶点)时,⊙O自身转动的角度恰好等于n边形在这个顶点的一个外角,根据多边形的外角和为360°,可得出⊙O滚动经过n个顶点自身又转动一圈,综上,当⊙O和凸n边形的周长相等时,⊙O自身转动了2圈.
解答:解:根据运动方式不同,分两种情况考虑:
(i)当一个圆沿着线段的一个端点无滑动地滚动到另一个端点,
圆自身转动的圈数=(线段的长度÷圆的周长),
若不考虑⊙O滚动经过n个顶点的情况,可得⊙O自身恰好转动了一圈;
(ii)当⊙O在某边的一端,滚动经过该端点(即顶点)时,
⊙O自身转动的角度恰好等于n边形在这个顶点的一个外角,
∵凸n边形的外角和为360°
∴⊙O滚动经过n个顶点自身又转动一圈,
综上,当⊙O和凸n边形的周长相等时,⊙O自身转动了2圈.
故选B.
(i)当一个圆沿着线段的一个端点无滑动地滚动到另一个端点,
圆自身转动的圈数=(线段的长度÷圆的周长),
若不考虑⊙O滚动经过n个顶点的情况,可得⊙O自身恰好转动了一圈;
(ii)当⊙O在某边的一端,滚动经过该端点(即顶点)时,
⊙O自身转动的角度恰好等于n边形在这个顶点的一个外角,
∵凸n边形的外角和为360°
∴⊙O滚动经过n个顶点自身又转动一圈,
综上,当⊙O和凸n边形的周长相等时,⊙O自身转动了2圈.
故选B.
点评:此题考查了直线与圆的位置关系,利用了分类讨论的思想,审清题意,总结出圆O两种运动方式的规律是解本题的关键.

练习册系列答案
相关题目
已知函数y=(a-2)x-3a-1,当自变量x的取值范围是3≤x≤5时,y既能达到大于5的值,又能取到小于3的值,则实数a的取值范围是( )
| A、a<3 | B、a>5 |
| C、a>8 | D、任意实数 |
数列x1,x2,…,x100满足下列条件:对于k=1,2,…,100,xk比其余99个数的和小k,已知x50=
,m,n是互质的正整数,则m+n等于( )
| m |
| n |
| A、50 | B、100 |
| C、165 | D、173 |
 已知点P是正方形ABCD内一点,且点P到A,B,D的距离分别为
已知点P是正方形ABCD内一点,且点P到A,B,D的距离分别为 如图,AB为⊙O的直径,弦CD⊥AB于E,∠CDB=15°,OE=2
如图,AB为⊙O的直径,弦CD⊥AB于E,∠CDB=15°,OE=2 如图,半圆O的半径为1,AC⊥AB,BD⊥AB,且AC=1,BD=3,P是半圆上任意一点,则封闭图形ABDPC面积的最大值是
如图,半圆O的半径为1,AC⊥AB,BD⊥AB,且AC=1,BD=3,P是半圆上任意一点,则封闭图形ABDPC面积的最大值是 如图,在平面直角坐标系中,△ABC的顶点A(-7,1),B(1,1)C(1,7),△DEF与△ABC关于原点对称,请画出△DEF与△ABC同时绕坐标原点O逆时针旋转90°的图形.
如图,在平面直角坐标系中,△ABC的顶点A(-7,1),B(1,1)C(1,7),△DEF与△ABC关于原点对称,请画出△DEF与△ABC同时绕坐标原点O逆时针旋转90°的图形.