题目内容
5. 如图所示,在△ABC中,AB=AC=10,BC=12.
如图所示,在△ABC中,AB=AC=10,BC=12.(1)用尺规作图作∠BAC的角平分线AD.(不要求写作法、证明,但保留作图痕迹);
(2)求△ABC的面积.
分析 (1)直接利用角平分线的作法得出AD;
(2)利用等腰三角形的性质以及勾股定理求出AD的长,进而得出答案.
解答  解:(1)如图所示:AD即为所求;
解:(1)如图所示:AD即为所求;
(2)∵AB=AC=10,BC=12,AD平分∠BAC,
∴AD⊥BC,且BD=DC=6,
∴AD=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
则△ABC的面积为:$\frac{1}{2}$×8×12=48.
点评 此题主要考查了基本作图以及等腰三角形的性质等知识,正确应用等腰三角形的性质是解题关键.

练习册系列答案
相关题目
20.设P=a2(-a+b-c),Q=-a(a2-ab+ac),则P与Q的关系是( )
| A. | P=Q | B. | P>Q | C. | P<Q | D. | 互为相反数 |
10.若a>0且ax=2,ay=3,则ax-2y的值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{9}$ |
14.计算3x6÷x2的结果是( )
| A. | 2x4 | B. | 2x3 | C. | 3x4 | D. | 3x3 |
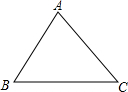 在如图所示的△ABC中.
在如图所示的△ABC中.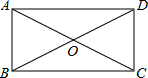 如图,矩形ABCD中,对角线AC与BD交于点O,∠BAC=60°,AC=10.
如图,矩形ABCD中,对角线AC与BD交于点O,∠BAC=60°,AC=10.