题目内容
15.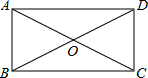 如图,矩形ABCD中,对角线AC与BD交于点O,∠BAC=60°,AC=10.
如图,矩形ABCD中,对角线AC与BD交于点O,∠BAC=60°,AC=10.(1)矩形的周长;
(2)求矩形的面积.
分析 (1)由矩形性质得出AD=BC,AB=CD,∠BAD=90°,OA=OC=$\frac{1}{2}$AC,BO=OD=$\frac{1}{2}$BD,AC=BD,推出OA=OB=OC=OD,得出等边三角形AOB,求出BD,由勾股定理求出AD即可;
(2)由矩形的面积公式即可得出结果.
解答 解:(1)∵四边形ABCD是矩形,
∴∠BAD=90°,BD=AC=10,OA=OC=$\frac{1}{2}$AC=5,BO=OD=$\frac{1}{2}$BD=5,
∴OA=OB=OC=OD,
∵∠BAC=60°,
∴△AOB是等边三角形,
∵AB=5,
∴OA=OB=AB=5,
∴BD=2OB=2,
在Rt△BAD中,AB=5,BD=10,
由勾股定理得:AD=$\sqrt{B{D}^{2}-A{B}^{2}}$=5$\sqrt{3}$,
∵四边形ABCD是矩形,
∴AB=CD=5,AD=BC=5$\sqrt{3}$,
∴矩形ABCD的周长=AB+BC+CD+AD=10+10$\sqrt{3}$;
(2)矩形的面积=AB×BC=5×5$\sqrt{3}$=25$\sqrt{3}$.
点评 本题考查了矩形性质,等边三角形的性质和判定,勾股定理等知识点;关键是求出AD的长,题目比较典型,是一道比较好的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.计算x3y2•(-xy3)2的结果是( )
| A. | x5y10 | B. | x5y7 | C. | -x5y10 | D. | x5y8 |
4.下列各数中最小的是( )
| A. | -2015 | B. | $\frac{1}{2015}$ | C. | -$\frac{1}{2015}$ | D. | 2015 |
 如图所示,在△ABC中,AB=AC=10,BC=12.
如图所示,在△ABC中,AB=AC=10,BC=12. 如图,在平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(3,1).
如图,在平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(3,1).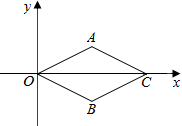 如图,以菱形AOBC的顶点O为原点,对角线OC所在直线为x轴建立平面直角坐标系,若OB=5,点C的坐标为(8,0),则点A的坐标为(4,3).
如图,以菱形AOBC的顶点O为原点,对角线OC所在直线为x轴建立平面直角坐标系,若OB=5,点C的坐标为(8,0),则点A的坐标为(4,3).