题目内容
2. 细心观察下图,认真分析各式,然后解答问题.
细心观察下图,认真分析各式,然后解答问题.OA22=($\sqrt{1}$)2+1=2 S1=$\frac{\sqrt{1}}{2}$;
OA32=12+($\sqrt{2}$)2=3 S2=$\frac{\sqrt{2}}{2}$;
OA42=12+($\sqrt{3}$)2=4 S3=$\frac{\sqrt{3}}{2}$
…
(1)(直接写出答案)OA10=$\sqrt{10}$.
(2)请用含有n(n是正整数)的等式表示上述变化规律.
(3)求出S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+S${\;}_{3}^{2}$+…+S${\;}_{10}^{2}$的值.
分析 (1)由给出的数据写出OA102的长,即可得出S10的值;
(2)由(1)OA12,OA22,OA33…和S1、S2、S3…Sn,找出规律即可得出结果;
(3)首先求出S12+S22+S32+…+Sn2的公式,然后把n=10代入即可.
解答 解:(1)∵OA12=1,OA22=2,OA32=3,…,
∴OA102=10,
∴OA10=$\sqrt{10}$;
故答案为:$\sqrt{10}$;
(2)由(1)得:OAn2=12+($\sqrt{n-1}$)2=n,Sn=$\frac{\sqrt{n}}{2}$;
(3)∵S12=$\frac{1}{4}$,S22=$\frac{2}{4}$,S32=$\frac{3}{4}$,…,S102=$\frac{10}{4}$,
∴S12+S22+S32+…+Sn2=$\frac{1}{4}+\frac{2}{4}+\frac{3}{4}+…+\frac{10}{4}$=$\frac{55}{4}$.
点评 本题主要考查勾股定理的知识点,解答本题的关键是熟练运用勾股定理,此题难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下面各组线段中,能组成三角形的是( )
| A. | 5,2,3 | B. | 10,5,4 | C. | 4,8,4 | D. | 2,3,4 |
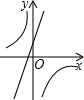
 如图,已知:CD=AB,∠BAD=∠BDA,AE是△ABD的中线,求证:AC=2AE.
如图,已知:CD=AB,∠BAD=∠BDA,AE是△ABD的中线,求证:AC=2AE.