题目内容
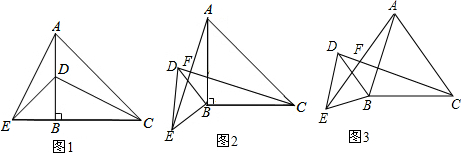
12.阅读:如图1,△ABC和△DBE中,AB=CB,DB=EB,∠ABC=∠DBE=90°,D点在AB上,连接AE,DC.求证:AE=CD,AE⊥CD.
证明:延长CD交AE于点F.∵AB=BC,BE=DB.∴Rt△AEB≌Rt△CDB.
∴AE=CD,∠EAB=∠DCB.∵∠DCB+∠CDB=90°,∠ADF=∠CDB.
∴∠ADF+∠DAF=90°.∴∠AFD=90°.∴AE⊥CD.
类比:
若将图1中的△DBE绕点B逆时针旋转一个锐角,如图2所示,问图2中的线段AE,CD之间的数量和位置关系还成立吗?若成立,请给予证明;若不成立,请说明理由.
拓展:
若将图1中的△DBE绕点B逆时针旋转一个锐角,将“∠ABC=∠DBE=90°”改为“∠ABC=∠DBE=α(α为锐角)”,其他条件均不变,如图3所示,问(直接回答问题结果,不要求写结论过程):
①图3中的线段AE,CD是否仍然相等?
②线段AE,CD的位置关系是否发生改变?若改变,其所在直线的夹角大小是否随着图形的旋转而发生变化?若不变化,其值多少?
分析 类比:根据∠DBE=∠ABC=90°,得出∠ABE=∠DBC,再证出△AEB≌△CDB,AE=CD,∠EAB=∠DCB,再根据∠DCB+∠COB=90°,∠AOF=∠COB,得出∠FOA+∠FAO=90°,∠AFC=90°,即可证出AE⊥CD;
拓展:①根据∠DBE=∠ABC=α,于是得到∠ABE=∠DBC,推出△AEB≌△CDB,即可得到结论;
②通过△AEB≌△CDB,根据全等三角形的性质得到∠EAB=∠DCB,由对顶角相等得到∠AHF=∠CHB,于是得到∠AFH=∠ABC=α.
解答 解:类比:AE=CD,AE⊥CD,
证明:∠DBE=∠ABC=90°,
∴∠ABE=∠DBC,
在△AEB和△CDB中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠DBC}\\{BE=BD}\end{array}\right.$,
∴△AEB≌△CDB,
∴AE=CD,∠EAB=∠DCB,
∵∠DCB+∠COB=90°,∠AOF=∠COB,
∴∠FOA+∠FAO=90°,
∴∠AFC=90°,
∴AE⊥CD;
拓展:①AE=CD,
∵∠DBE=∠ABC=α,
∴∠ABE=∠DBC,
在△AEB和△CDB中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠DBC}\\{BE=BD}\end{array}\right.$,
∴△AEB≌△CDB,
∴AE=CD;
②线段AE,CD的位置关系发生改变,其所在直线的夹角大小不随着图形的旋转而发生变化,
∵△AEB≌△CDB,
∴∠EAB=∠DCB,
∵∠AHF=∠CHB,
∴∠AFH=∠ABC=α,
∴线段AE,CD的位置关系发生改变,其所在直线的夹角大小不随着图形的旋转而发生变化.
点评 此题考查了全等三角形的判定与性质,用到的知识点全等三角形的判定与性质,关键是能在较复杂的图形中找出全等的三角形.

 阅读快车系列答案
阅读快车系列答案 如图是某个几何体的平面展开图,这个几何体是( )
如图是某个几何体的平面展开图,这个几何体是( )| A. | 三棱柱 | B. | 长方体 | C. | 圆柱 | D. | 球 |
| A. | y=3x2+4 | B. | y=-$\frac{1}{3}{x^2}$ | C. | y=(x+1)(x-2) | D. | y=$\sqrt{x^2}$ |
 细心观察下图,认真分析各式,然后解答问题.
细心观察下图,认真分析各式,然后解答问题.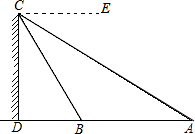 如图,A、B两点与建筑物底部D在同一直线上,从建筑物顶部C点测得∠ECA=30°,∠ECB=60°,且AB=20,求建筑物CD的高.
如图,A、B两点与建筑物底部D在同一直线上,从建筑物顶部C点测得∠ECA=30°,∠ECB=60°,且AB=20,求建筑物CD的高. 小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数共有5个.
小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数共有5个.