题目内容
17.已知x、y为实数且$\sqrt{x-1}$+|2y+1|=0,则x+y=$\frac{1}{2}$.分析 根据非负数的性质列式求出x、y,然后代入代数式进行计算即可得解.
解答 解:由题意得,x-1=0,2y+1=0,
解得x=1,y=-$\frac{1}{2}$,
所以,x+y=1+(-$\frac{1}{2}$)=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目
6.如果m-n=3,mn=1,那么m2+n2的值是( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
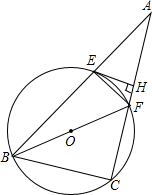 已知:如图,⊙O过△ABC的B、C两点,分别交AB、AC于点E、F.
已知:如图,⊙O过△ABC的B、C两点,分别交AB、AC于点E、F.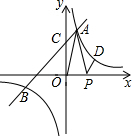 如图所示,直线y=2x+3与双曲线y=$\frac{m}{x}$相交于A,B两点,与轴交于点C,且△OCA的面积为1.5.
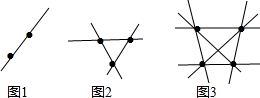
如图所示,直线y=2x+3与双曲线y=$\frac{m}{x}$相交于A,B两点,与轴交于点C,且△OCA的面积为1.5. 细心观察下图,认真分析各式,然后解答问题.
细心观察下图,认真分析各式,然后解答问题.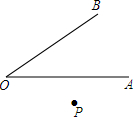 已知:如图,在∠AOB外有一点P,
已知:如图,在∠AOB外有一点P,