题目内容
5.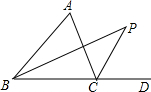 已知,如图,在△ABC中,BP是∠ABC的角平分线,CP是∠ACD的平分线,∠P=35°,求∠A.
已知,如图,在△ABC中,BP是∠ABC的角平分线,CP是∠ACD的平分线,∠P=35°,求∠A.
分析 根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠PCD=∠P+∠PBC,根据角平分线的定义可得∠PBC=$\frac{1}{2}$∠ABC,∠PCD=$\frac{1}{2}$∠ACD,然后整理得到∠A=2∠P.
解答 解:由三角形的外角性质得,∠ACD=∠A+∠ABC,∠PCD=∠P+∠PBC,
∵∠ABC的平分线BP和外角∠ACD的平分线CP相交于点P,
∴∠PBC=$\frac{1}{2}$∠ABC,∠PCD=$\frac{1}{2}$∠ACD,
∴∠P+$\frac{1}{2}$∠ABC=$\frac{1}{2}$(∠A+∠ABC),
∴∠A=2∠P,
∵∠P=35°,
∴∠A=2×35°=70°.
点评 本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
相关题目
13.商店某种货物的进价下降了8%,但销售价不变,于是货物的销售利润($\frac{销售价-进价}{进价}$×100%)由原来的r%增加到(r+10)%,则r的值等于( )
| A. | 12 | B. | 15 | C. | 25 | D. | 50 |
20.下列各式中,去括号不正确的是( )
| A. | 6(-x+$\frac{1}{2}$xy)=-6x+3xy | B. | -2(a-3b)=-2a+6b | ||
| C. | -(-1+3x)=-1-3x | D. | 3-(-2xy+5y)=3+2xy-5y |
17.某项工程,甲单独做20小时完成,乙单独做21小时完成,现由甲单独做5小时,剩下的甲、乙合做,还需几小时完成?若设剩下的部分要x小时完成,下列方程正确的是( )
| A. | $\frac{5}{20}$-$\frac{x}{20}$-$\frac{x}{21}$=1 | B. | $\frac{5}{20}$+$\frac{x}{20}$-$\frac{x}{21}$=1 | C. | $\frac{5}{20}$+$\frac{x}{20}$+$\frac{x}{21}$=1 | D. | $\frac{5}{20}$-$\frac{x}{20}$+$\frac{x}{21}$=1 |
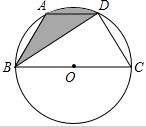 如图,已知点A、B、C、D均在已知圆上,AD∥BC,BD平分∠ABC,∠BAD=120°,四边形ABD的周长为15.
如图,已知点A、B、C、D均在已知圆上,AD∥BC,BD平分∠ABC,∠BAD=120°,四边形ABD的周长为15.