题目内容
10.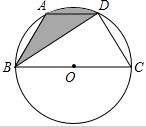 如图,已知点A、B、C、D均在已知圆上,AD∥BC,BD平分∠ABC,∠BAD=120°,四边形ABD的周长为15.
如图,已知点A、B、C、D均在已知圆上,AD∥BC,BD平分∠ABC,∠BAD=120°,四边形ABD的周长为15.(1)求此圆的半径;
(2)求图中阴影部分的面积.
分析 (1)先根据平行线的性质得出$\widehat{AB}$=$\widehat{CD}$,故可得出∠ABC=∠C=60°,连接OA,OB,可得出△OCD,△OAB与△OAD均为等边三角形,故可得出AD=AB=CD=3,由此可得出结论;
(2)由(1)知,AD=AB=OB=OA=3,故可得出四边形ABOD是菱形,再由SAS定理得出△ABE≌△ODE,故S阴影=S扇形AOD,由此可得出结论.
解答 解:(1)∵AD∥BC,∠C=60°,
$\widehat{AB}$=$\widehat{CD}$,
∴∠ABC=∠C=60°.
连接OA,OB,
∵OC=OD=3,∠C=60°,
∴△OCD是等边三角形.
同理可得,△OAB与△OAD均为等边三角形,
∴圆的半径是3;
(2)∵由(1)知,AD=AB=OB=OA=3,
∴四边形ABOD是菱形,
∴AE=OE,BE=DE,
在△ABE与△ODE中,
$\left\{\begin{array}{l}{AE=OE}\\{∠AEB=∠OED}\\{BE=DE}\end{array}\right.$,
∴△ABE≌△ODE(SAS),
∴S阴影=S扇形AOD=$\frac{60π×{3}^{2}}{360}$=$\frac{3}{2}$π.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
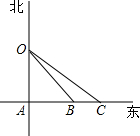 如图,有A、B、C三个村庄,A庄在某市的市中心正南方40km处,B、C两个村庄在A庄的正东方向上,且距A庄分别为30km和35km,该市中心有一座信息发射塔(即O点),覆盖半径为50km,问三个村庄A、B、C是否能收到该塔发出的信息.
如图,有A、B、C三个村庄,A庄在某市的市中心正南方40km处,B、C两个村庄在A庄的正东方向上,且距A庄分别为30km和35km,该市中心有一座信息发射塔(即O点),覆盖半径为50km,问三个村庄A、B、C是否能收到该塔发出的信息.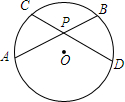 如图,已知⊙O的弦AB,CD相交于点P,PO平分∠APD,求证:AB=CD.
如图,已知⊙O的弦AB,CD相交于点P,PO平分∠APD,求证:AB=CD.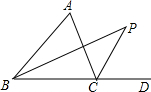 已知,如图,在△ABC中,BP是∠ABC的角平分线,CP是∠ACD的平分线,∠P=35°,求∠A.
已知,如图,在△ABC中,BP是∠ABC的角平分线,CP是∠ACD的平分线,∠P=35°,求∠A. 如图,在△ABC中,∠C=90°,AB的中点为点O.求证:A、B、C三点在以点0为圆心的圆上.
如图,在△ABC中,∠C=90°,AB的中点为点O.求证:A、B、C三点在以点0为圆心的圆上.