题目内容
4.已知$\frac{x}{y+z+u}$=$\frac{y}{z+u+x}$=$\frac{z}{u+x+y}$=$\frac{u}{x+y+z}$,求$\frac{x+y}{z+u}$+$\frac{y+z}{u+x}$+$\frac{z+u}{x+y}$+$\frac{u+x}{y+z}$的值.分析 设$\frac{x}{y+z+u}$=$\frac{y}{z+u+x}$=$\frac{z}{u+x+y}$=$\frac{u}{x+y+z}$=$\frac{1}{t}$,可得y+z+u=tx,z+u+x=ty,u+x+y=tz,x+y+z=tu,四式相加得:3(x+y+z+u)=t(x+y+z+u),分两种情况当x+y+z+u=0时,当x+y+z+u≠0时,t=3时分别求解即可.
解答 解:设$\frac{x}{y+z+u}$=$\frac{y}{z+u+x}$=$\frac{z}{u+x+y}$=$\frac{u}{x+y+z}$=$\frac{1}{t}$,
∴y+z+u=tx,z+u+x=ty,u+x+y=tz,x+y+z=tu,
四式相加得:3(x+y+z+u)=t(x+y+z+u),
当x+y+z+u=0时,$\frac{x+y}{z+u}$+$\frac{y+z}{u+x}$+$\frac{z+u}{x+y}$+$\frac{u+x}{y+z}$=$\frac{-(z+u)}{z+u}$+$\frac{-(u+x)}{u+x}$+$\frac{-(x+y)}{x+y}$+$\frac{-(y+z)}{y+z}$=-4,
当x+y+z+u≠0时,t=3,
∴y+z+u=3x,z+u+x=3y,u+x+y=3z,x+y+z=3u,
前两个式子相减得y-x=3(x-y),得x=y,
同理可得y=z,z=u,u=x,
∴x=y=z=u,
∴$\frac{x+y}{z+u}$+$\frac{y+z}{u+x}$+$\frac{z+u}{x+y}$+$\frac{u+x}{y+z}$=4,
综上所述:$\frac{x+y}{z+u}$+$\frac{y+z}{u+x}$+$\frac{z+u}{x+y}$+$\frac{u+x}{y+z}$=4或-4.
点评 本题主要考查了分式的化简求值,解题的关键是设$\frac{x}{y+z+u}$=$\frac{y}{z+u+x}$=$\frac{z}{u+x+y}$=$\frac{u}{x+y+z}$=$\frac{1}{t}$,分两种情况求解.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案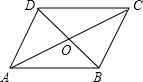 如图,?ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )
如图,?ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )| A. | 1<m<11 | B. | 2<m<22 | C. | 10<m<12 | D. | 5<m<6 |
 梯形的上底长12cm,高15cm,阴影部分面积为15cm2,求梯形的面积.
梯形的上底长12cm,高15cm,阴影部分面积为15cm2,求梯形的面积. 已知AB∥CD,直线MN分别交AB,CD于E、F,∠MFD=50°,EG平分∠MEB,求∠MEG的度数.
已知AB∥CD,直线MN分别交AB,CD于E、F,∠MFD=50°,EG平分∠MEB,求∠MEG的度数. 如图,由点A(a,0),O(0,0),B(-a,a+3)(a>0),确定的△AOB的面积为2,求a的值.
如图,由点A(a,0),O(0,0),B(-a,a+3)(a>0),确定的△AOB的面积为2,求a的值.