题目内容
12. 梯形的上底长12cm,高15cm,阴影部分面积为15cm2,求梯形的面积.
梯形的上底长12cm,高15cm,阴影部分面积为15cm2,求梯形的面积.
分析 连接AE得到四边形ABCE是梯形,于是得到S△AFE=S△BFC=15,进一步得到S△AFB=$\frac{1}{2}×12×15-15$=75,根据同高三角形的面积比等于底的比得到$\frac{BF}{EF}$=$\frac{1}{3}$,于是求得S△CFE=$\frac{1}{3}$S△BCF=3,即可求得结果.
解答  解:连接AE,
解:连接AE,
∵四边形ABCD是梯形,
∴AB∥CD,
∴四边形ABCE是梯形,
∴S△AFE=S△BFC=15,
∴S△AFB=$\frac{1}{2}×12×15-15$=75,
∴$\frac{BF}{EF}$=$\frac{{S}_{△ABF}}{{S}_{△AFE}}$=$\frac{75}{15}$=3,
∴S△CFE=$\frac{1}{3}$S△BCF=3,
∴S梯形ABCD=S矩形ABED+S△BCE=12×15+15+3=198.
点评 本题考查了梯形的面积的求法,三角形的面积的求法,知道同高不同底的三角形面积的比等于底的比是解题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
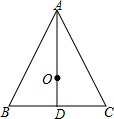 已知等边三角形边长为a,点O是△ABC的重心,求AO,OD的长.
已知等边三角形边长为a,点O是△ABC的重心,求AO,OD的长.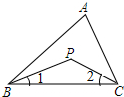 如图,P是△ABC内一点,连结PB、PC.
如图,P是△ABC内一点,连结PB、PC. 求图中阴影部分的面积.
求图中阴影部分的面积.