题目内容
14. 如图,由点A(a,0),O(0,0),B(-a,a+3)(a>0),确定的△AOB的面积为2,求a的值.
如图,由点A(a,0),O(0,0),B(-a,a+3)(a>0),确定的△AOB的面积为2,求a的值.
分析 根据三角形的面积公式,可得关于a的一元二次方程,根据解方程,可得答案.
解答 解:由△AOB的面积为2,得$\frac{1}{2}$a(a+3)=2.
化简,得a2+3a-4=0,
解得a=-3(不符合题意要舍去),a=1.
点评 本题考查了坐标与图形的性质,利用三角形的面积公式得出关于a的一元二次方程是解题关键.

练习册系列答案
相关题目
2.计算:
(1)$\sqrt{13}$($\sqrt{13}$+$\frac{5}{\sqrt{13}}$);
(2)2$\sqrt{3}$-$\root{3}{8}$-|2-2$\sqrt{3}$|.
(1)$\sqrt{13}$($\sqrt{13}$+$\frac{5}{\sqrt{13}}$);
(2)2$\sqrt{3}$-$\root{3}{8}$-|2-2$\sqrt{3}$|.
9.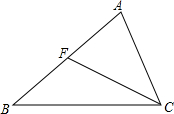 如图,F是△ABC的AB边上一点,下列结论正确的个数是( )
如图,F是△ABC的AB边上一点,下列结论正确的个数是( )
①若∠AFC=∠ACB,则△ACF∽△ABC
②若∠AFC=∠B,则△ACF∽△ABC
③若AC2=AF•AB,则△ACF∽△ABC
④若AC:CF=AB:BC,则△ACF∽△ABC.
 如图,F是△ABC的AB边上一点,下列结论正确的个数是( )
如图,F是△ABC的AB边上一点,下列结论正确的个数是( )①若∠AFC=∠ACB,则△ACF∽△ABC
②若∠AFC=∠B,则△ACF∽△ABC
③若AC2=AF•AB,则△ACF∽△ABC
④若AC:CF=AB:BC,则△ACF∽△ABC.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
6.已知下列各数,10,5.314,-$\frac{1}{3}$,0.74,π.其中无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.已知关于x的分式方程$\frac{x+k}{x+1}$-$\frac{k}{x-1}$=1的解为负数,则k的取值范围是( )
| A. | k>$\frac{1}{2}$或k≠1 | B. | k>$\frac{1}{2}$且k≠1 | C. | k<$\frac{1}{2}$且k≠1 | D. | k<$\frac{1}{2}$或k≠1 |
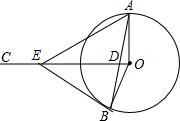 如图,OA、OB是⊙O的半径,过点O作OC⊥OA,交弦AB于点D,点E是BD的垂直平分线与OC的交点,连接BE
如图,OA、OB是⊙O的半径,过点O作OC⊥OA,交弦AB于点D,点E是BD的垂直平分线与OC的交点,连接BE