题目内容
1.先化简,再求值:$\frac{m-3}{{3{m^2}-9m}}÷\frac{1}{{3{m^2}}}$,其中m是二次函数y=(x+2)2-3顶点的纵坐标.分析 利用根据分式的乘除法进行化简,再由抛物线的顶点坐标可求得m的值,代入求值即可.
解答 解:
∵二次函数y=(x+2)2-3顶点的纵坐标是(-2,-3),
∴m=-3,
∵$\frac{m-3}{{3{m^2}-9m}}÷\frac{1}{{3{m^2}}}$=$\frac{m-3}{3m(m-3)}•3{m^2}=m$,
∴当m=-3时,原式=m=-3.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为x=h,顶点坐标为(h,k).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.把二次函数y=x2-2x+4化为y=a(x-h)2+k的形式,下列变形正确的是( )
| A. | y=(x+1)2+3 | B. | y=(x-2)2+3 | C. | y=(x-1)2+5 | D. | y=(x-1)2+3 |
6.-0.5的倒数是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
13.以下列各组长度的三条线段为边,能组成三角形的是( )
| A. | 1cm,2cm,3cm | B. | 8cm,6cm,4cm | C. | 12cm,5cm,6cm | D. | 2cm,3cm,6cm |
10.当a=1时,a-2a+3a-4a+…+99a-100a的值为( )
| A. | 5050 | B. | 100 | C. | -50 | D. | 50 |
1.一元二次方程2x2+8x=0的解是( )
| A. | x1=x2=4 | B. | x1=x2=0 | C. | x1=0,x2=4 | D. | x1=0,x2=-4 |
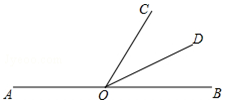 如图,点A、O、B在一条直线上,∠AOC=130°,OD是∠BOC的平分线,则∠COD=25度.
如图,点A、O、B在一条直线上,∠AOC=130°,OD是∠BOC的平分线,则∠COD=25度. 如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数y=$\frac{12}{x}$(x>0)图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数y=$\frac{12}{x}$(x>0)图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.