题目内容
9. 如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数y=$\frac{12}{x}$(x>0)图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数y=$\frac{12}{x}$(x>0)图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.(1)求证:P为线段AB的中点;
(2)求△AOB的面积.
分析 (1)利用圆周角定理的推论得出AB是⊙P的直径即可;
(2)首先假设点P坐标为(m,n)(m>0,n>0),得出OA=2OM=2m,OB=2ON=2n,进而利用三角形面积公式求出即可.
解答 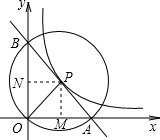 (1)证明:∵点A、O、B在⊙P上,且∠AOB=90°,
(1)证明:∵点A、O、B在⊙P上,且∠AOB=90°,
∴AB为⊙P直径,
即P为AB中点;
(2)解:∵P为$y=\frac{12}{x}$(x>0)上的点,
设点P的坐标为(m,n),则mn=12,
过点P作PM⊥x轴于M,PN⊥y轴于N,
∴M的坐标为(m,0),N的坐标为(0,n),
且OM=m,ON=n,
∵点A、O、B在⊙P上,
∴M为OA中点,OA=2 m;
N为OB中点,OB=2 n,
∴S△AOB=$\frac{1}{2}$OA•O B=2mn=24.
点评 此题主要考查了反比例函数综合以及三角形面积求法和圆周角定理推论等知识,熟练利用反比例函数的性质得出OA,OB的长是解题关键.

练习册系列答案
相关题目
17.下列函数中是反比例函数的是( )
| A. | $y=\frac{x}{3}$ | B. | $y=\frac{3}{x+1}$ | C. | $y=\frac{x^2}{2}$ | D. | $y=\frac{3}{2x}$ |
4. 在同一坐标系下,抛物线y1=-x2+4x和直线y2=2x的图象如图所示,那么不等式-x2+4x>2x的解集是( )
在同一坐标系下,抛物线y1=-x2+4x和直线y2=2x的图象如图所示,那么不等式-x2+4x>2x的解集是( )
 在同一坐标系下,抛物线y1=-x2+4x和直线y2=2x的图象如图所示,那么不等式-x2+4x>2x的解集是( )
在同一坐标系下,抛物线y1=-x2+4x和直线y2=2x的图象如图所示,那么不等式-x2+4x>2x的解集是( )| A. | x<0 | B. | 0<x<2 | C. | x>2 | D. | x<0或 x>2 |
14.如果⊙O的半径为7cm,圆心O到直线l的距离为d,且d=5cm,那么⊙O和直线l的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不确定 |
18.下列说法正确的是( )
| A. | 延长射线OA | B. | 延长直线AB | C. | 延长线段AB | D. | 作直线AB=CD |
9.下列关于画图的语句正确的是( )
| A. | 画直线AB=8cm | |
| B. | 画射线OA=8cm | |
| C. | 已知A、B、C三点,过这三点画一条直线 | |
| D. | 过直线AB外一点画一直线与AB平行 |
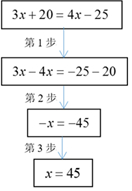 下面的框图表示解方程3x+20=4x-25的流程.第1步的依据是等式两边加(或减)同一个数(或式子),结果仍相等.
下面的框图表示解方程3x+20=4x-25的流程.第1步的依据是等式两边加(或减)同一个数(或式子),结果仍相等. 已知抛物线y=$\frac{1}{5}$x2+$\frac{2}{5}$mx+$\frac{1}{5}$m2+m+3的顶点A在一条直线l上运动.
已知抛物线y=$\frac{1}{5}$x2+$\frac{2}{5}$mx+$\frac{1}{5}$m2+m+3的顶点A在一条直线l上运动.