题目内容
19.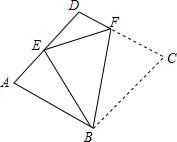 一个棱长为a的菱形ABCD,E是AD的中点,将此图形沿BF折叠,点C恰好与点E重合,如图.求tanA的值.
一个棱长为a的菱形ABCD,E是AD的中点,将此图形沿BF折叠,点C恰好与点E重合,如图.求tanA的值.
分析 取AE的中点G,连接BG,根据折叠的性质和菱形的性质可知AG⊥BG,AG=$\frac{1}{4}$a,根据勾股定理求出BG,再根据正切定义计算即可.
解答 解:取AE的中点G,连接BG,
由题意知菱形ABCD的边长为a,则AB=BE=a,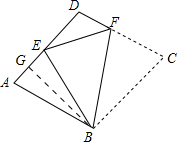
∴AG⊥BG,AG=$\frac{1}{4}$a,
在Rt△ABG中,BG=$\sqrt{A{B}^{2}-A{G}^{2}}$=$\sqrt{{a}^{2}-(\frac{1}{4}a)^{2}}$=$\frac{\sqrt{15}}{4}$a,
∴tanA=$\frac{BG}{AG}$=$\frac{\frac{\sqrt{15}}{4}a}{\frac{1}{4}a}$=$\sqrt{15}$.
点评 本题主要考查了菱形的性质和折叠的性质以及勾股定理和锐角三角函数定义,作辅助线构造直角三角形是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.能判定四边形是菱形的条件是( )
| A. | 两条对角线相等 | B. | 两条对角线相互垂直 | ||
| C. | 两条对角线相互垂直平分 | D. | 两条对角线相等且垂直 |
4. 为了让广大青少年学生走向操场、走进自然,走到阳光下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”,短跑运动,可以锻炼人的灵活性,增强人的爆发力.因此张明和王亮在课外活动中,报名参加了短跑训练小组在近几次百米训练中,所测成绩如图所示.请根据图中所示,解答以下问题.
为了让广大青少年学生走向操场、走进自然,走到阳光下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”,短跑运动,可以锻炼人的灵活性,增强人的爆发力.因此张明和王亮在课外活动中,报名参加了短跑训练小组在近几次百米训练中,所测成绩如图所示.请根据图中所示,解答以下问题.
(1)请根据图中信息,补齐上面的表格;
(2)从图中看,张明与王亮哪次的成绩最好?
(3)分别计算张明,王亮的平均数和方差.
 为了让广大青少年学生走向操场、走进自然,走到阳光下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”,短跑运动,可以锻炼人的灵活性,增强人的爆发力.因此张明和王亮在课外活动中,报名参加了短跑训练小组在近几次百米训练中,所测成绩如图所示.请根据图中所示,解答以下问题.
为了让广大青少年学生走向操场、走进自然,走到阳光下,积极参加体育锻炼,我国启动了“全国亿万学生阳光体育运动”,短跑运动,可以锻炼人的灵活性,增强人的爆发力.因此张明和王亮在课外活动中,报名参加了短跑训练小组在近几次百米训练中,所测成绩如图所示.请根据图中所示,解答以下问题.| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 张明 | 13.3 | 13.4 | 13.3 | 13.2 | 13.3 |
| 王亮 | 13.2 | 13.4 | 13.1 | 13.5 | 13.3 |
(2)从图中看,张明与王亮哪次的成绩最好?
(3)分别计算张明,王亮的平均数和方差.
11.直线y=-2x-2和直线y=x+4的图象与x轴所围成的三角形的面积为( )
| A. | 12 | B. | 6 | C. | 3 | D. | $\frac{3}{2}$ |
8.若二次根式$\sqrt{3x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x<$\frac{2}{3}$ | B. | x≤$\frac{2}{3}$ | C. | x>$\frac{2}{3}$ | D. | x≥$\frac{2}{3}$ |
 如图,矩形OABC,OA=9,AB=15,点E是BC上一点,沿AE折叠,使点B恰好落在x轴的点D处.
如图,矩形OABC,OA=9,AB=15,点E是BC上一点,沿AE折叠,使点B恰好落在x轴的点D处.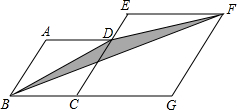 如图,菱形ABCD和菱形ECGF的边长分别为3和4,∠A=120°,则图中阴影部分的面积$\frac{9\sqrt{3}}{4}$.
如图,菱形ABCD和菱形ECGF的边长分别为3和4,∠A=120°,则图中阴影部分的面积$\frac{9\sqrt{3}}{4}$. 已知AB∥DE,∠B=60°,且CM平分∠DCB,CM⊥CN,垂足为C,求∠NCE的度数.
已知AB∥DE,∠B=60°,且CM平分∠DCB,CM⊥CN,垂足为C,求∠NCE的度数.