题目内容
9. 已知AB∥DE,∠B=60°,且CM平分∠DCB,CM⊥CN,垂足为C,求∠NCE的度数.
已知AB∥DE,∠B=60°,且CM平分∠DCB,CM⊥CN,垂足为C,求∠NCE的度数.
分析 先根据平行线的性质得出∠BCD的度数,再由角平分线的定义求出∠DCM的度数,根据CM⊥CN可知∠MCN=90°,故∠DCM+∠NCE=90°,由此可得出结论.
解答 解:∵AB∥DE,∠B=60°,
∴∠BCD=120°.
∵CM平分∠DCB,
∴∠DCM=$\frac{1}{2}$∠DCB=60°.
∵CM⊥CN,
∴∠MCN=90°,
∴∠DCM+∠NCE=90°,
∴∠NCE=90°-60°=30°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
相关题目
17.下列说法错误的是( )
| A. | 9的算术平方根是3 | B. | 16的平方根是±4 | ||
| C. | 27的立方根是±3 | D. | 立方根等于-1的实数是-1 |
14.二元一次方程组$\left\{\begin{array}{l}{3x+2y=6}\\{y=x-2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-\frac{3}{2}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-\frac{3}{2}}\\{y=\frac{1}{2}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=0}\\{y=-2}\end{array}\right.$ |
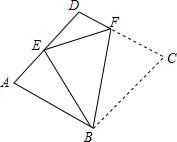 一个棱长为a的菱形ABCD,E是AD的中点,将此图形沿BF折叠,点C恰好与点E重合,如图.求tanA的值.
一个棱长为a的菱形ABCD,E是AD的中点,将此图形沿BF折叠,点C恰好与点E重合,如图.求tanA的值.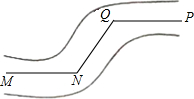 如图,一条公路两次转弯后又回到原来的方向,如果第一次转弯时∠N=120°,则第二次转弯时∠Q=120°.
如图,一条公路两次转弯后又回到原来的方向,如果第一次转弯时∠N=120°,则第二次转弯时∠Q=120°. 如图,已知平行四边形ABCD中,对角线AC的垂直平分线EF交AD于点F,交BC于点E,试判断:四边形AECF是什么特殊四边形,并说明理由.
如图,已知平行四边形ABCD中,对角线AC的垂直平分线EF交AD于点F,交BC于点E,试判断:四边形AECF是什么特殊四边形,并说明理由.