题目内容
14.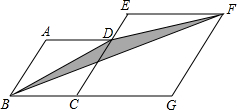 如图,菱形ABCD和菱形ECGF的边长分别为3和4,∠A=120°,则图中阴影部分的面积$\frac{9\sqrt{3}}{4}$.
如图,菱形ABCD和菱形ECGF的边长分别为3和4,∠A=120°,则图中阴影部分的面积$\frac{9\sqrt{3}}{4}$.
分析 作BM⊥FG于M,交EC于N,如图,根据菱形的性质得BC=CD=3,CG=GF=4,AB∥CE∥GF,∠ABC=∠BCD=∠CGF=120°,则∠BCN=∠BGM=60°,再根据含30度的直角三角形三边的关系,在Rt△BCN中可计算出BN=$\sqrt{3}$CN=$\frac{3\sqrt{3}}{2}$,在Rt△BMG中可计算出BM=$\sqrt{3}$GM=$\frac{7\sqrt{3}}{2}$,则MN=BM-BN=$\frac{7\sqrt{3}}{2}$-$\frac{3\sqrt{3}}{2}$=2$\sqrt{3}$,然后根据三角形面积公式和梯形面积公式,利用S阴影部分=S△BCD+S梯形CDFG-S△BGF进行计算即可.另一种解法为把阴影部分的面积转化为△BCD的面积进行计算.
解答 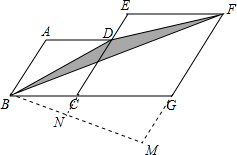 解:作BM⊥FG于M,交EC于N,如图,
解:作BM⊥FG于M,交EC于N,如图,
∵四边形ABCD和四边形CGFE为菱形,
∴BC=CD=3,CG=GF=4,AB∥CE∥GF,
∴∠ABC=∠BCD=∠CGF=120°,
∴∠BCN=∠BGM=60°,
∵BM⊥GF,
∴BN⊥EC,
在Rt△BCN中,∵∠NBC=30°,
∴CN=$\frac{1}{2}$BC=$\frac{3}{2}$,
BN=$\sqrt{3}$CN=$\frac{3\sqrt{3}}{2}$,
在Rt△BMG中,GM=$\frac{1}{2}$BG=$\frac{7}{2}$,
BM=$\sqrt{3}$GM=$\frac{7\sqrt{3}}{2}$,
∴MN=BM-BN=$\frac{7\sqrt{3}}{2}$-$\frac{3\sqrt{3}}{2}$=2$\sqrt{3}$,
∴S阴影部分=S△BCD+S梯形CDFG-S△BGF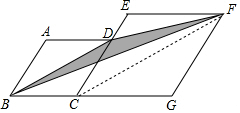
=$\frac{1}{2}$×3×$\frac{3\sqrt{3}}{2}$+$\frac{1}{2}$×(3+4)×2$\sqrt{3}$-$\frac{1}{2}$×4×$\frac{7\sqrt{3}}{2}$
=$\frac{9\sqrt{3}}{4}$.
另一种解法:连接CF,如图,
∵四边形ABCD和四边形CGFE为菱形,∠A=120°,
∴∠DBC=∠FCG=30°,
∴BD∥CF,
∴S△FDB=S△CDB=$\frac{1}{2}$S菱形ABCD=$\frac{1}{2}$•2•$\frac{\sqrt{3}}{4}$•32=$\frac{9\sqrt{3}}{4}$.
故答案为$\frac{9\sqrt{3}}{4}$.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.利用面积的和差计算不规则图形的面积是解决此题的关键,记住含30度的直角三角形三边的关系.

 考前必练系列答案
考前必练系列答案| A. | SAS | B. | SSS | C. | ASA | D. | ASA或AAS |
 星期天,小王五朋友家借书,如图是他离家的距离y(千米)与时间x(分钟)的关系图象.根据图象信息,下列说法正确的是( )
星期天,小王五朋友家借书,如图是他离家的距离y(千米)与时间x(分钟)的关系图象.根据图象信息,下列说法正确的是( )| A. | 小王去时的速度大于回家的速度 | |
| B. | 小王在朋友家停留了10分钟 | |
| C. | 小王去时花的时间少于回家时所花的时间 | |
| D. | 小王去时走下坡路,回家时走上坡路 |
| A. | a3•(-3a2)=-3a6 | B. | 6(b-a)2-2(a-b)=2(a-b)(3a-3b-1) | ||
| C. | (-2a-3b)(2a-3b)=4a2-9b2 | D. | (-a)6÷(-a)3=a2 |
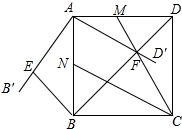 如图,在正方形ABCD中,AB=2$\sqrt{2}$,将∠BAD绕着点A顺时针旋转α°(0<α<45°),得到∠B′AD′,其中射线AB′与过点B且与对角线BD垂直的直线交于点E,射线AD′与对角线BD交于点F,连接CF,并延长交AD于点M,作∠BCM的角平分线交AB于点N,当满足S四边形AEBF=$\sqrt{2}$S△CDM时,线段BN的长度为2$\sqrt{3}$-2.
如图,在正方形ABCD中,AB=2$\sqrt{2}$,将∠BAD绕着点A顺时针旋转α°(0<α<45°),得到∠B′AD′,其中射线AB′与过点B且与对角线BD垂直的直线交于点E,射线AD′与对角线BD交于点F,连接CF,并延长交AD于点M,作∠BCM的角平分线交AB于点N,当满足S四边形AEBF=$\sqrt{2}$S△CDM时,线段BN的长度为2$\sqrt{3}$-2.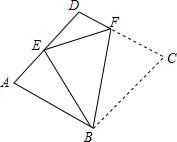 一个棱长为a的菱形ABCD,E是AD的中点,将此图形沿BF折叠,点C恰好与点E重合,如图.求tanA的值.
一个棱长为a的菱形ABCD,E是AD的中点,将此图形沿BF折叠,点C恰好与点E重合,如图.求tanA的值.