题目内容
14.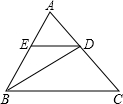 如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,则∠BED的度数是( )
如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,则∠BED的度数是( )| A. | 35° | B. | 70° | C. | 110° | D. | 130° |
分析 由三角形的外角性质得出∠ABD=35°,由角平分线的定义求出∠ABC=2∠ABD=70°,再由平行线的性质得出同旁内角互补∠BED+∠ABC=180°,即可得出结果.
解答 解:∵∠BDC=∠A+∠ABD,
∴∠ABD=95°-60°=35°,
∵BD是∠ABC的角平分线,
∴∠ABC=2∠ABD=70°,
∵DE∥BC,
∴∠BED+∠ABC=180°,
∴∠BED=180°-70°=110°.
故选C.
点评 本题考查了平行线的性质、三角形的外角性质;熟练掌握平行线的性质,运用三角形的外角性质求出∠ABD的度数是解决问题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
5.下列说法中,不正确的是( )
| A. | 没有最小的有理数 | |
| B. | 互为相反数的两个数到原点的距离相等 | |
| C. | 零没有相反数 | |
| D. | 最大的负整数是-1 |
19.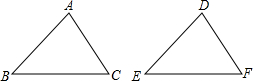 如图,在△ABC和△DEF中,∠B=∠E,∠C=∠F,若要使△ABC≌△DEF,则可添加的条件为( )
如图,在△ABC和△DEF中,∠B=∠E,∠C=∠F,若要使△ABC≌△DEF,则可添加的条件为( )
 如图,在△ABC和△DEF中,∠B=∠E,∠C=∠F,若要使△ABC≌△DEF,则可添加的条件为( )
如图,在△ABC和△DEF中,∠B=∠E,∠C=∠F,若要使△ABC≌△DEF,则可添加的条件为( )| A. | BC=EF | B. | AB=DF | C. | AC=DE | D. | ∠A=∠D |
4. a,b两数在数轴上的位置如图所示,下列结论正确的是( )
a,b两数在数轴上的位置如图所示,下列结论正确的是( )
 a,b两数在数轴上的位置如图所示,下列结论正确的是( )
a,b两数在数轴上的位置如图所示,下列结论正确的是( )| A. | ab>0 | B. | a>b>1 | C. | a+b<0 | D. | a-b<0 |
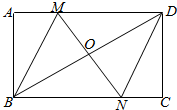 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连BM,DN.
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连BM,DN.