题目内容
4.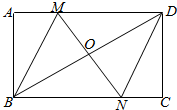 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连BM,DN.
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连BM,DN.(1)求证:四边形BMDN为菱形;
(2)若AB=4,AD=8,求Sin∠ABM的值.
分析 (1)由AAS证明△MOD≌△NOB,得出MO=NO,证出四边形BNDM是平行四边形,再由MN⊥BD,即可得出四边形BNDM为菱形;
(2)由菱形的性质得出BM=MD,BM=MD=x,则AM=8-x,由勾股定理得出方程,解方程求出BM、AM,即可得出结果.
解答 (1)证明:∵四边形ABCD为矩形,
∴MD∥BN,
∴∠MDO=∠NBO,
又MN平分BO,
∴BO=DO,
在△MOD和△NOB中,$\left\{\begin{array}{l}{∠MDO=∠NBO}&{\;}\\{∠MOD=∠NOB}&{\;}\\{OD=OB}&{\;}\end{array}\right.$,
∴△MOD≌△NOB(AAS),
∴MO=NO,
∴四边形BNDM是平行四边形,
又MN⊥BD,
∵四边形BNDM为菱形;
(2)解:由(1)得:四边形BNDM为菱形,
∴BM=MD,
设BM=MD=x,则AM=8-x,
在△ABM中,由勾股定理得:
42+(8-x)2=x2
解得:x=5,
∴BM=5,AM=3,
∴sin∠ABM=$\frac{AM}{BM}=\frac{3}{5}$
点评 本题考查了矩形的性质、全等三角形的判定与性质、菱形的判定与性质、勾股定理;熟练掌握矩形的性质和菱形的判定方法,证明四边形是菱形是解决问题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
14.一个三角形的面积是$\frac{4}{5}$平方米,其中一条边是2米,这边上的高是( )
| A. | $\frac{8}{5}$米 | B. | $\frac{4}{5}$米 | C. | $\frac{2}{5}$米 | D. | 2米 |
15.一元二次方程2x2-7x-5=0的两根分别是x1,x2,则x1x2等于( )
| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -$\frac{7}{2}$ | D. | -$\frac{5}{2}$ |
9.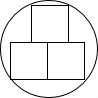 如图,三个全等的正方形内接于圆,正方形的边长为16,则圆的半径为( )
如图,三个全等的正方形内接于圆,正方形的边长为16,则圆的半径为( )
 如图,三个全等的正方形内接于圆,正方形的边长为16,则圆的半径为( )
如图,三个全等的正方形内接于圆,正方形的边长为16,则圆的半径为( )| A. | $3\sqrt{33}$ | B. | $16\sqrt{5}$ | C. | $16\sqrt{2}$ | D. | $5\sqrt{17}$ |
13.一元二次方程3x2-7x-12=0的二次项、一次项和常数项分别是( )
| A. | 3x2,7x,12 | B. | 3x2,-7x,12 | C. | 3x2,7x,-12 | D. | 3x2,-7x,-12 |
14.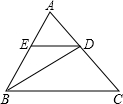 如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,则∠BED的度数是( )
如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,则∠BED的度数是( )
 如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,则∠BED的度数是( )
如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,则∠BED的度数是( )| A. | 35° | B. | 70° | C. | 110° | D. | 130° |
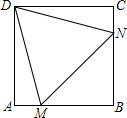 如图,在正方形ABCD中,等边三角形DMN的顶点M、N分别在AB和BC上,若等边三角形DMN的边长为$2\sqrt{2}$,则正方形ABCD的边长为1+$\sqrt{3}$.
如图,在正方形ABCD中,等边三角形DMN的顶点M、N分别在AB和BC上,若等边三角形DMN的边长为$2\sqrt{2}$,则正方形ABCD的边长为1+$\sqrt{3}$.