题目内容
实数a满足丨a丨+a=0，且a≠-1，那么
= 或 ．
| |a|-1 |
| |a+1| |
考点：分式的化简求值,绝对值
专题：计算题
分析：根据实数a满足丨a丨+a=0，且a≠-1，可求出a=0或者a＜0，然后代入即可求解．
解答：解：实数a满足丨a丨+a=0，且a≠-1，
∴a=0或者a＜0，且a≠-1，
当a=0时，代入
=
=-1．
当-1＜a＜0且a≠-1时，代入
=-1，
当a＜-1时，代入
=
=1．
综上所述：当-1＜a≤0时，原式=-1；
当a＜-1时，原式=1．
故答案为：-1或1．
∴a=0或者a＜0，且a≠-1，
当a=0时，代入
| |a|-1 |
| |a+1| |
| -1 |
| 1 |
当-1＜a＜0且a≠-1时，代入
| |a|-1 |
| |a+1| |
当a＜-1时，代入
| |a|-1 |
| |a+1| |
| -a-1 |
| -a-1 |
综上所述：当-1＜a≤0时，原式=-1；
当a＜-1时，原式=1．
故答案为：-1或1．
点评：本题考查了分式的化简求值及绝对值的性质，难度适中，关键是分类讨论a的取值范围．
练习册系列答案
相关题目
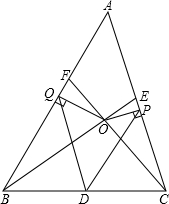如图，在△ABC中，D为BC的中点，点E、F分别在边AC、AB上，并且∠ABE=∠ACF，BE、CF交于点O．过点O作OP⊥AC，OQ⊥AB，P、Q为垂足．求证：DP=DQ．