题目内容
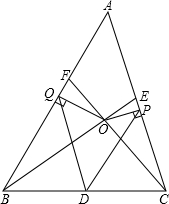 如图,在△ABC中,D为BC的中点,点E、F分别在边AC、AB上,并且∠ABE=∠ACF,BE、CF交于点O.过点O作OP⊥AC,OQ⊥AB,P、Q为垂足.求证:DP=DQ.
如图,在△ABC中,D为BC的中点,点E、F分别在边AC、AB上,并且∠ABE=∠ACF,BE、CF交于点O.过点O作OP⊥AC,OQ⊥AB,P、Q为垂足.求证:DP=DQ.考点:三角形中位线定理,全等三角形的判定与性质
专题:证明题
分析:取OB中点M,OC中点N,根据三角形中位线定理可得到DM∥OC,DM=
OC,DN∥OB,DN=
OB,再根据直角三角形斜边上的中线的性质得到QM=
OB,PN=
OC,再根据三角形外角的性质即可推出∠QMD=∠PND,从而利用SAS判定△QMD≌△DNP,根据全等三角形的对应的边相等即可证得结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 证明:如图,取OB中点M,OC中点N,连接MD,MQ,DN,PN.
证明:如图,取OB中点M,OC中点N,连接MD,MQ,DN,PN.
∵D为BC的中点
∴DM∥OC,DM=
OC,DN∥OB,DN=
OB.
∵在Rt△BOQ和Rt△OCP中,QM=
OB,PN=
OC.
∴DM=PN,QM=DN.∠QMD=∠QMO+∠OMD=2∠ABO+∠FOB,
∠PND=∠PNO+∠OND=2∠ACO+∠EOC.
∵∠ABO=∠ACO,∠FOB=∠EOC,
∴∠QMD=∠PND.
∴△QMD≌△DNP,
∴DQ=DP.
 证明:如图,取OB中点M,OC中点N,连接MD,MQ,DN,PN.
证明:如图,取OB中点M,OC中点N,连接MD,MQ,DN,PN.∵D为BC的中点
∴DM∥OC,DM=
| 1 |
| 2 |
| 1 |
| 2 |
∵在Rt△BOQ和Rt△OCP中,QM=
| 1 |
| 2 |
| 1 |
| 2 |
∴DM=PN,QM=DN.∠QMD=∠QMO+∠OMD=2∠ABO+∠FOB,
∠PND=∠PNO+∠OND=2∠ACO+∠EOC.
∵∠ABO=∠ACO,∠FOB=∠EOC,
∴∠QMD=∠PND.
∴△QMD≌△DNP,
∴DQ=DP.
点评:此题主要考查学生对三角形中位线定理及全等三角形的判定与性质的综合运用能力.

练习册系列答案
相关题目
已知三角形三个内角的度数之比为x:y:z,且x+y<z,则这个三角形是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
方程|x-|2x+1||=3的解的个数是( )
| A、0个 | B、1个 | C、2个 | D、无穷多 |
a为有理数,则一定成立的关系式是( )
| A、7a>a | B、7+a>a |
| C、7+a>7 | D、|a|≥7 |
有一串数:-2003,-1999,-1995,-1991,┉,按一定的规律排列,那么这串数中前( )个数的和最小.
| A、500 | B、501 |
| C、502 | D、503 |
 如图,已知边长为a的正方形ABCD,E为AD的中点,P为CE的中点,那么△BPD的面积的值是
如图,已知边长为a的正方形ABCD,E为AD的中点,P为CE的中点,那么△BPD的面积的值是