题目内容
15.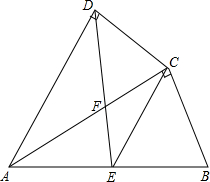 如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD;∠ADC=90°,E为AB的中点,
如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD;∠ADC=90°,E为AB的中点,(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由.
分析 (1)证明∠DAC=∠CAB,∠ADC=∠ACB=90,即可解决问题;
(2)根据直角三角形的性质,可得CE与AE的关系,根据等腰三角形的性质,可得∠EAC=∠ECA,根据角平分线的定义,可得∠CAD=∠CAB,根据平行线的判定,可得答案.
解答 证明:(1)∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB.
(2)CE∥AD;
∵E是AB的中点,
∴CE=$\frac{1}{2}$AB=AE,
∴∠EAC=∠ECA.
∵AC平分∠DAB,
∴∠CAD=∠CAB,
∴CAD=∠ECA,
∴CE∥AD.
点评 该题主要考查了直角三角形的性质、相似三角形的判定及其性质等几何知识点及其应用问题;牢固掌握直角三角形的性质、相似三角形的判定及其性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.若关于x的不等式组$\left\{\begin{array}{l}{10-5x≥0}\\{9x≥2x+m}\end{array}\right.$无解,则实数m的取值范围是( )
| A. | m≤14 | B. | m<14 | C. | m≥14 | D. | m>14 |
10.关于一元二次方程x2+(4k+1)x+2k-1=0,说法正确的是( )
| A. | 一定有两个相等的实数根 | B. | 一定有实数根 | ||
| C. | 一定有两个不相等的实数根 | D. | 一定没有实数根 |
4.下列各式中,正确的是( )
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | (-$\sqrt{3}$)2=9 | C. | $\root{3}{-9}$=-3 | D. | ±$\sqrt{9}$=±3 |
5.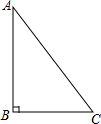 如图,在Rt△ABC中,∠B=90°,∠BAC=40°,AB=7,则AC的长为( )
如图,在Rt△ABC中,∠B=90°,∠BAC=40°,AB=7,则AC的长为( )
 如图,在Rt△ABC中,∠B=90°,∠BAC=40°,AB=7,则AC的长为( )
如图,在Rt△ABC中,∠B=90°,∠BAC=40°,AB=7,则AC的长为( )| A. | $\frac{7}{sin40°}$ | B. | $\frac{7}{tan40°}$ | C. | 7cos40° | D. | $\frac{7}{cos40°}$ |
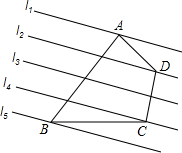 如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是$\frac{17}{2}$.
如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是$\frac{17}{2}$.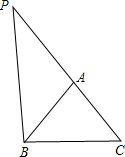 在△ABC中,AB=6,BC=8,CA=7,延长CA至点P,使∠PBA=∠C,则AP=9.
在△ABC中,AB=6,BC=8,CA=7,延长CA至点P,使∠PBA=∠C,则AP=9. △ABC和点S都在正方形网格的格点上,每个小正方形的边长为1.
△ABC和点S都在正方形网格的格点上,每个小正方形的边长为1.