题目内容
5.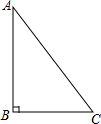 如图,在Rt△ABC中,∠B=90°,∠BAC=40°,AB=7,则AC的长为( )
如图,在Rt△ABC中,∠B=90°,∠BAC=40°,AB=7,则AC的长为( )| A. | $\frac{7}{sin40°}$ | B. | $\frac{7}{tan40°}$ | C. | 7cos40° | D. | $\frac{7}{cos40°}$ |
分析 在Rt△ABC中,利用余弦函数的定义可得cos∠BAC=$\frac{AB}{AC}$,即AC=$\frac{AB}{cos∠BAC}$,将数值代入即可.
解答 解:∵在Rt△ABC中,∠B=90°,
∴cos∠BAC=$\frac{AB}{AC}$,即AC=$\frac{AB}{cos∠BAC}$,
∵∠BAC=40°,AB=7,
∴AC=$\frac{7}{cos40°}$.
故选D.
点评 本题考查了解直角三角形,解直角三角形要用到的关系(在Rt△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边):
①锐角直角的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:sinA=∠A的对边:斜边=a:c,cosA=∠A的邻边:斜边=b:c,tanA=∠A的对边:∠A的邻边=a:b.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
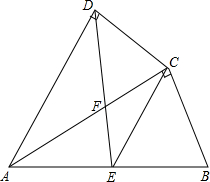 如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD;∠ADC=90°,E为AB的中点,
如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD;∠ADC=90°,E为AB的中点,
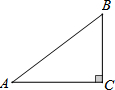 如图,△ABC中∠ACB=90°,AC=8cm,BC=6cm
如图,△ABC中∠ACB=90°,AC=8cm,BC=6cm