题目内容
20.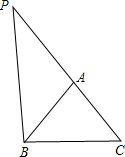 在△ABC中,AB=6,BC=8,CA=7,延长CA至点P,使∠PBA=∠C,则AP=9.
在△ABC中,AB=6,BC=8,CA=7,延长CA至点P,使∠PBA=∠C,则AP=9.
分析 由∠PBC=∠C,∠P=∠P,得到△PAB∽△PBC,得到$\frac{PA}{PB}$=$\frac{PB}{PC}$=$\frac{AB}{BC}$,设PA=x,PB=y,代入数值即可求出.
解答 解:∵∠PBC=∠C,∠P=∠P,
∴△PAB∽△PBC,
∴$\frac{PA}{PB}$=$\frac{PB}{PC}$=$\frac{AB}{BC}$,
设PA=x,PB=y,
∴$\frac{x}{y}$=$\frac{y}{x+7}$=$\frac{6}{8}$,
解得:x=9,
∴PA=9.
故答案为:9.
点评 本题考查了相似三角形的判定和性质,列出二元一次方程组是解题的关键.

练习册系列答案
相关题目
13.若不等式2x<6的解都能使关于x的一次不等式(a-1)x<a+7成立,则a的取值范围是( )
| A. | 1<a≤5 | B. | a≤5 | C. | a<1或a≥5 | D. | a=5 |
 已知数a、b、c在数轴上的位置如图所示,化简|a+b|-|a-b|+|a+c|.
已知数a、b、c在数轴上的位置如图所示,化简|a+b|-|a-b|+|a+c|.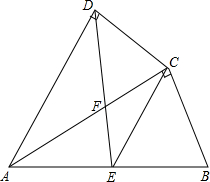 如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD;∠ADC=90°,E为AB的中点,
如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD;∠ADC=90°,E为AB的中点, 已知:如图,AB∥CD,AC与BD相交于E,若CE=2,AE=3,AB=5,BD=$\frac{20}{3}$,求sinA的值.
已知:如图,AB∥CD,AC与BD相交于E,若CE=2,AE=3,AB=5,BD=$\frac{20}{3}$,求sinA的值.