题目内容
9.设A=$\frac{x-3}{2}$+3,B=x+1,x为何值时,(1)A>B;
(2)A=B;
(3)A<B?
分析 (1)根据A>B列出关于x的不等式,求出x取值范围即可;
(2)根据A=B列出关于x的方程,求出x的值即可;
(3)根据A<B列出关于x的不等式,求出x取值范围即可.
解答 解:(1)∵A=$\frac{x-3}{2}$+3,B=x+1,A>B,
∴$\frac{x-3}{2}$+3>x+1,解得x<1;
(2)∵A=$\frac{x-3}{2}$+3,B=x+1,A>B,
∴$\frac{x-3}{2}$+3=x+1,解得x=1;
(3)∵A=$\frac{x-3}{2}$+3,B=x+1,A>B,
∴$\frac{x-3}{2}$+3<x+1,解得x>1.
点评 本题考查的是解一元一次不等式,熟知不等式的基本性质是解答此题的关键.

练习册系列答案
相关题目
17.经过两点A(2,3)、B(-4,3)作直线AB,则直线AB( )
| A. | 平行于x轴 | B. | 平行于y轴 | C. | 经过原点 | D. | 以上说法都不对 |
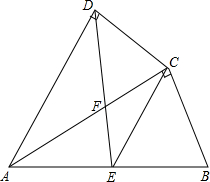 如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD;∠ADC=90°,E为AB的中点,
如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD;∠ADC=90°,E为AB的中点,