题目内容
8.若关于x的不等式组$\left\{\begin{array}{l}{10-5x≥0}\\{9x≥2x+m}\end{array}\right.$无解,则实数m的取值范围是( )| A. | m≤14 | B. | m<14 | C. | m≥14 | D. | m>14 |
分析 分别解两个不等式得到x≤2和x≥$\frac{m}{7}$,根据大大小小找不到得2<$\frac{m}{7}$,然后解关于m的一元一次不等式即可.
解答 解:$\left\{\begin{array}{l}{10-5x≥0①}\\{9x≥2x+m②}\end{array}\right.$,
解①得x≤2,
解②得x≥$\frac{m}{7}$,
因为不等式组无解,
所以2<$\frac{m}{7}$,
所以m>14.
故选D.
点评 本题考查了解不等式组:求不等式组的解集的过程叫解不等式组.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
18.把一元二次方程x2-6x+4=0化成(x+n)2=m的形式时,m+n的值为( )
| A. | 8 | B. | 6 | C. | 3 | D. | 2 |
16.下列运算正确的是( )
| A. | a6÷a2=a8 | B. | 3x2•5x3=15x5 | C. | (-3a2b)2=-6a4b2 | D. | (3a+b)(3a-b)=3a2-b2 |
3.某学校的复印任务由甲复印社承接,其收费y(元)与复印页数x(页)的关系如表:
(1)表格中反映的变量是复印页数、收费,其中自变量是复印页数,因变量是收费;
(2)随着复印页数x的逐渐增加,其收费y的变化趋势是什么?
(3)复印页数x每增加100页,收费y怎样变化?
(4)当复印页数为2000页时,其收费y是多少元?
| x(页) | 100 | 200 | 400 | 1000 | … |
| y(元) | 40 | 80 | 160 | 400 | … |
(2)随着复印页数x的逐渐增加,其收费y的变化趋势是什么?
(3)复印页数x每增加100页,收费y怎样变化?
(4)当复印页数为2000页时,其收费y是多少元?
13.若不等式2x<6的解都能使关于x的一次不等式(a-1)x<a+7成立,则a的取值范围是( )
| A. | 1<a≤5 | B. | a≤5 | C. | a<1或a≥5 | D. | a=5 |
17.经过两点A(2,3)、B(-4,3)作直线AB,则直线AB( )
| A. | 平行于x轴 | B. | 平行于y轴 | C. | 经过原点 | D. | 以上说法都不对 |
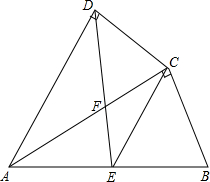 如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD;∠ADC=90°,E为AB的中点,
如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD;∠ADC=90°,E为AB的中点,