题目内容
8.已知木棒AB垂直投射于投影面α上的投影为A1B1,且木棒AB的长为8cm(1)如图(1),若AB平行于投影面α,求A1B1长;
(2)如图(2),若木棒AB与投影面α的倾斜角为30°,求这时A1B1长.
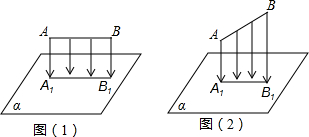
分析 (1)由平行投影性质:平行长不变,可得A1B1=AB;
(2)过A作AH⊥BB1,在Rt△ABH中有AH=ABcos30°,可得A1B1的长度.
解答 解:(1)由于是平行投影,故A1B1=AB=8cm;
(2)过A作AH⊥BB1,垂足为H.
∵AA1⊥A1B1,BB1⊥A1B1,
∴四边形AA1B1H为矩形,
∴AH=A1B1,
在Rt△ABH中,∵∠BAH=30°,AB=8 cm,
∴AH=ABcos30°=8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$(cm).即A1B1=4$\sqrt{3}$cm.
点评 本题主要考查平行投影的性质,线段的平行投影性质:平行长不变、倾斜长缩短、垂直成一点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列各组中,是二元一次方程x+2y=3的解的是( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=\frac{2}{3}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ |
17.方程2x-3y=5,xy=3,x2+y=6中二元一次方程有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
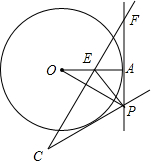 如图,P是⊙O的切线FA上的点,点A为切点,连接OP,OP的垂直平分线FE交OA于点E,连接EP,过点P作PC⊥EP
如图,P是⊙O的切线FA上的点,点A为切点,连接OP,OP的垂直平分线FE交OA于点E,连接EP,过点P作PC⊥EP 如图所示,某居民小区的A,B两楼之间的距离MN=30m,两楼高都是20m,A楼在B楼正南,B楼一楼朝南的窗台离地面的距离CN=2m,窗户高1.8m,正午时刻太阳光线与地面成30°角,A楼的影子是否影响B楼一楼窗户采光?若影响,挡住窗户多高?若不影响,请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
如图所示,某居民小区的A,B两楼之间的距离MN=30m,两楼高都是20m,A楼在B楼正南,B楼一楼朝南的窗台离地面的距离CN=2m,窗户高1.8m,正午时刻太阳光线与地面成30°角,A楼的影子是否影响B楼一楼窗户采光?若影响,挡住窗户多高?若不影响,请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)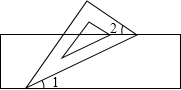 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是35°.
如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是35°. 某工厂要制作一个容积为300立方厘米的正方体形状的无盖水槽(如图所示).准备用钢板焊制,试求至少要用多少平方厘米的钢板?(结果精确到1平方厘米)
某工厂要制作一个容积为300立方厘米的正方体形状的无盖水槽(如图所示).准备用钢板焊制,试求至少要用多少平方厘米的钢板?(结果精确到1平方厘米)