题目内容
11.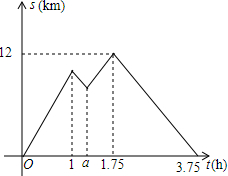 淆明小长假,李梅陋父母一起去青岛游玩.他们乘坐了一艘可远行12km的船在海上观光,该船远行时顺流匀速行驶.返回时则逆流匀速行驶.远行途中.李梅发现自己携带的游泳圈不知何时落入水中,于是该船立刻原路返回,一刻钟后找到游泳圈,随后继续远行,行驶到离出发地12km远的地方后没有停留又立刻返回.已知游泳圈的漂流速度和水流速度相同,船在远行和返回途中的静水速度相间.船与出发地的距离s(km)与行驶时间t(h)之间的函数图象如图所示.
淆明小长假,李梅陋父母一起去青岛游玩.他们乘坐了一艘可远行12km的船在海上观光,该船远行时顺流匀速行驶.返回时则逆流匀速行驶.远行途中.李梅发现自己携带的游泳圈不知何时落入水中,于是该船立刻原路返回,一刻钟后找到游泳圈,随后继续远行,行驶到离出发地12km远的地方后没有停留又立刻返回.已知游泳圈的漂流速度和水流速度相同,船在远行和返回途中的静水速度相间.船与出发地的距离s(km)与行驶时间t(h)之间的函数图象如图所示.(1)a的值为1.25h;船在远行途中,逆流行驶了13.5km.
(2)求船在静水中的速度;
(3)求船在远行途中,s与t之间的函数关系式;
(4)求游泳圈刚落入水中时的s.
分析 (1)船在静水中的速度是akm/h,水流的速度是bkm/h,则顺流速度是(a+b)km/h,逆流的速度是(a-b)km/h,根据路程是12海里即可列方程求得;
(2)根据(1)即可直接求得;
(3)利用待定系数法即可求解;
(4)设船开出x小时后,游泳圈落入水中,则游泳圈在水中漂流的时间是(1+$\frac{1}{4}$-x)h,根据游泳圈漂到被找到时经过的距离与船直接从出发点到找到游泳圈的路程相等,从而列出方程求解.
解答 解:(1)设船在静水中的速度是akm/h,水流的速度是bkm/h,则顺流速度是(a+b)km/h,逆流的速度是(a-b)km/h,
根据题意得,返航(逆流)所用的时间是2h,从起航(顺流)到目的地所用时间是1.75小时,
而实际顺流航行的时间是(1.75-$\frac{1}{4}$)小时,多走的路程是找游泳圈的路程的$\frac{1}{4}$(a-b),
则$\left\{\begin{array}{l}{2(a-b)=12}\\{(1.75-\frac{1}{4})(a+b)-\frac{1}{4}(a-b)=12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=7.5}\\{b=1}\end{array}\right.$,
则a=1.25,逆流行驶的路程是(7.5-1.5)×(2+$\frac{1}{4}$)=13.5(km).
故答案是:1.25,13.5;
(2)船在静水中的速度是7.5km/h;
(3)由图可知,A的坐标是(1.75,12),B的坐标是(3.75,0),C的坐标是(1,9),D的坐标是(1.25,7.5).
当t≤1时,s=9t;
当1<t≤1.25时,s=-6t+15;
当1.25<t≤1.75时,s=9t-$\frac{15}{4}$;
当1.75<t≤3.75时,s=-6t+$\frac{45}{2}$;
(4)如图,
设船开出x小时后,游泳圈落入水中,则游泳圈在水中漂流的时间是(1+$\frac{1}{4}$-x)h,
根据题意得:(7.5+1.5)x+1.5(1+$\frac{1}{4}$-x)+$\frac{1}{4}$(7.5-1.5)=(7.5+1.5)×1,
解得:x=$\frac{3}{4}$,即船开出45分钟后,游泳圈落水.
点评 本题考查了一次函数的应用,正确读懂题目中的函数图象,列方程求得静水中的速度和水流的速度是关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=\frac{2}{3}}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ |
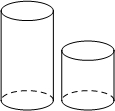 图中的两个圆柱体底面半径相同而高度不同,关于这两个圆柱体的视图说法正确的是( )
图中的两个圆柱体底面半径相同而高度不同,关于这两个圆柱体的视图说法正确的是( )| A. | 俯视图相同 | B. | 主视图、俯视图、左视图都相同 | ||
| C. | 左视图相同 | D. | 主视图相同 |
 如图,一次函数y=kx-2的图象与反比例函数的图象交于A、B两点,过A作AC⊥x轴于点C,己知cos∠AOC=$\frac{2\sqrt{5}}{5}$,OA=$\sqrt{5}$
如图,一次函数y=kx-2的图象与反比例函数的图象交于A、B两点,过A作AC⊥x轴于点C,己知cos∠AOC=$\frac{2\sqrt{5}}{5}$,OA=$\sqrt{5}$
 如图所示,某居民小区的A,B两楼之间的距离MN=30m,两楼高都是20m,A楼在B楼正南,B楼一楼朝南的窗台离地面的距离CN=2m,窗户高1.8m,正午时刻太阳光线与地面成30°角,A楼的影子是否影响B楼一楼窗户采光?若影响,挡住窗户多高?若不影响,请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
如图所示,某居民小区的A,B两楼之间的距离MN=30m,两楼高都是20m,A楼在B楼正南,B楼一楼朝南的窗台离地面的距离CN=2m,窗户高1.8m,正午时刻太阳光线与地面成30°角,A楼的影子是否影响B楼一楼窗户采光?若影响,挡住窗户多高?若不影响,请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)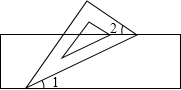 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是35°.
如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是35°.