题目内容
15.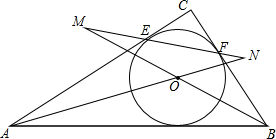 在Rt△ABC中,∠C=90°,它的内切圆⊙O分别与边AC、BC相切于点E、F,射线BO、A0交直线EF于点M、N,求证:$\frac{1}{5}$<$\frac{{S}_{△OMN}}{{S}_{△ABC}}$<$\frac{1}{4}$.
在Rt△ABC中,∠C=90°,它的内切圆⊙O分别与边AC、BC相切于点E、F,射线BO、A0交直线EF于点M、N,求证:$\frac{1}{5}$<$\frac{{S}_{△OMN}}{{S}_{△ABC}}$<$\frac{1}{4}$.
分析 根据∠C=90°,它的内切圆⊙O分别与边AC、BC相切于点E、F,于是得到△CEF是等腰直角三角形,根据等腰直角三角形的性质得到∠CEF=∠CFE=45°,由对顶角的性质得到∠NFB=∠CFE=45°,∠MEA=∠CEF=45°,根据外角的性质得到∠NOB=∠AOM=∠OAB+∠OBA=$\frac{1}{2}$(∠CAB+∠CBA)=45°,于是得到∠M=∠CAN=∠OAB,∠N=∠CBM=∠OBA,推出△NOM∽△AOB,根据相似三角形的性质得到$\frac{{S}_{△MON}}{{S}_{△AOB}}$=($\frac{\frac{1}{2}OC}{r}$)2=($\frac{\frac{\sqrt{2}}{2}r}{r}$)=$\frac{1}{2}$,通过整式的化简即可得到结论.
解答 解:∵∠C=90°,它的内切圆⊙O分别与边AC、BC相切于点E、F,
∴△CEF是等腰直角三角形,
∴∠CEF=∠CFE=45°,
∴∠NFB=∠CFE=45°,∠MEA=∠CEF=45°,
∴∠NOB=∠AOM=∠OAB+∠OBA=$\frac{1}{2}$(∠CAB+∠CBA)=45°,
∴∠M=∠CAN=∠OAB,∠N=∠CBM=∠OBA,
∴△NOM∽△AOB,
∴$\frac{{S}_{△MON}}{{S}_{△AOB}}$=($\frac{\frac{1}{2}OC}{r}$)2=($\frac{\frac{\sqrt{2}}{2}r}{r}$)=$\frac{1}{2}$,
∴$\frac{{S}_{△MON}}{{S}_{△AOB}}$=$\frac{\frac{1}{2}{S}_{△AOB}}{{S}_{△ABC}}$=$\frac{\frac{1}{2}×\frac{1}{2}•AB•r}{\frac{1}{2}•AB•h}$=$\frac{r}{2h}$,
∵$\frac{r}{2h}≥\frac{r}{2(\sqrt{2}+1)r}$=$\frac{\sqrt{2}-1}{2}$>$\frac{1}{5}$$\frac{r}{2h}<\frac{r}{2×2r}$=$\frac{1}{4}$,(h>2r)
∴$\frac{1}{5}$<$\frac{{S}_{△OMN}}{{S}_{△ABC}}$<$\frac{1}{4}$.
点评 本题考查了三角形的内切圆与内心,相似三角形的判定和性质,三角形的面积,熟练掌握三角形的内切圆的性质是解题的关键.

 ABC考王全优卷系列答案
ABC考王全优卷系列答案| A. | (x2)3=x6 | B. | a4•a3=a12 | C. | (ab)2=a2b2 | D. | (-a)3=-a3 |
 如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4.B为线段OA的中点.直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合).PQ∥y轴与抛物线交于点Q.
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4.B为线段OA的中点.直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合).PQ∥y轴与抛物线交于点Q.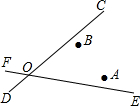 如图,直线CD、EF相交于O,求一点P,使P到直线CD、EF的距离相等,且到A、B两点的距离相等(先说出点的位置,尺规作图,不写作法,保留作图痕迹).
如图,直线CD、EF相交于O,求一点P,使P到直线CD、EF的距离相等,且到A、B两点的距离相等(先说出点的位置,尺规作图,不写作法,保留作图痕迹). 宽度都是a的两张纸条(对边平行)重叠在一起,如图所示.当夹角α=45°时,求阴影部分的面积.
宽度都是a的两张纸条(对边平行)重叠在一起,如图所示.当夹角α=45°时,求阴影部分的面积. 如图,每个小正方形都是边长为1个单位长度的正方形,△ABC与△A1B1C1是以点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
如图,每个小正方形都是边长为1个单位长度的正方形,△ABC与△A1B1C1是以点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.