题目内容
12. 已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.
已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.(1)猜想:∠B的度数,并证明你的猜想.
(2)如果AC=3cm,CD=2cm,求△ABD的面积.
分析 (1)根据已知条件得到AD=BD,由等腰三角形的性质得到∠B=∠DAE,根据AD是△ABC的角平分线,求得∠DAE=∠DAC,于是得到∠B=∠DAE=∠DAC,列方程即可得到结论;
(2)根据已知条件求得Rt△ACD≌Rt△AED,根据全等三角形的性质得到AE=BE,于是得到AB=2AE=2×3=6,即可得到结论.
解答 解:(1)猜想:∠B=30°,
∵DE⊥AB且AE=BE,
∴AD=BD,
∴∠B=∠DAE,
∵AD是△ABC的角平分线,
∴∠DAE=∠DAC,
∴∠B=∠DAE=∠DAC,
∵∠C=90°,
∴∠B+∠DAE+∠DAC=90°,
∴∠B=30°;
(2)∵∠C=90°,AD是△ABC的角平分线,DE⊥AB,
在Rt△ACD与Rt△AED中,
$\left\{\begin{array}{l}{CD=DE}\\{AD=AD}\end{array}\right.$,
∴Rt△ACD≌Rt△AED,
∴AE=BE,
∴AB=2AE=2×3=6,
∴S△ABD=$\frac{1}{2}$AB•DE=$\frac{1}{2}$×6×2=6cm2.
点评 本题考查了全等三角形的判定和性质,角平分线的性质,三角形的面积的求法,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
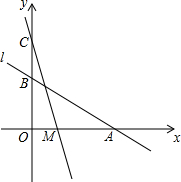 如图,直线L:y=-$\frac{1}{2}x+2$与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
如图,直线L:y=-$\frac{1}{2}x+2$与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.

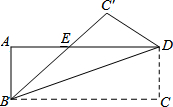 如图,长方形ABCD中,AB=4,BC=8,将长方形沿BC折叠,点C落在C′处.△BDE的面积是多少?
如图,长方形ABCD中,AB=4,BC=8,将长方形沿BC折叠,点C落在C′处.△BDE的面积是多少?