题目内容
2.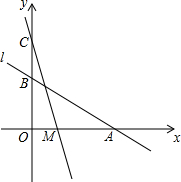 如图,直线L:y=-$\frac{1}{2}x+2$与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
如图,直线L:y=-$\frac{1}{2}x+2$与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.(1)当△COM的面积为4时,求点M的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式.
分析 (1)根据C的坐标求得OC=4,然后根据三角形COM的面积为4,求得OM=2,即可求得M的坐标;
(2)由直线AB的函数解析式,令y=0求A点坐标,由面积公式S=$\frac{1}{2}$×OM×OC,求出S与t之间的函数关系式.
解答 解:(1)∵C(0,4),
∴OC=4,
∵△COM的面积为4,
∴$\frac{1}{2}$OM•OC=4,
∴OM=2,
∴M(2,0)或(-2,0);
(2)∵C(0,4),A(4,0),
∴OC=OA=4,
当0≤t≤4时,OM=OA-AM=4-t,
S△OCM=$\frac{1}{2}$×4×(4-t)=8-2t;
当t>4时,OM=AM-OA=t-4,
S△OCM=$\frac{1}{2}$×4×(t-4)=2t-8.
∴△COM的面积S与M的移动时间t之间的函数关系式为:S=$\left\{\begin{array}{l}{8-2t(0≤t≤4)}\\{2t-8(t>4)}\end{array}\right.$.
点评 此题考查了一次函数图象上点的坐标特征,三角形的面积,进行分类讨论是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.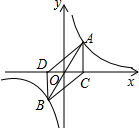 如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
 如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )| A. | S=2 | B. | 2<S<4 | C. | S=4 | D. | S>4 |
 已知反比例函数y=$\frac{6}{x}$在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB且AO=AB,则S△AOB=6.
已知反比例函数y=$\frac{6}{x}$在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB且AO=AB,则S△AOB=6.
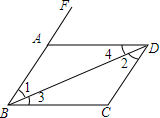 按图填空,并在横线内标明理由:
按图填空,并在横线内标明理由: 已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.
已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.