题目内容
3.解方程:(1)x(2x-5)=4x-10
(2)2x2-x-1=0
(3)x2+10x+9=0.
分析 (1)首先把方程右边分解因式,然后再移项,提公因式2x-5,可得(2x-5)(x-2)=0,再解即可;
(2)首先把方程左边分解因式可得(2x+1)(x-1)=0,进而可得一元一次方程2x+1=0,x-1=0,再解即可;
(3)首先把方程左边分解因式可得(x+9)(x+1)=0,进而可得一元一次方程x+9=0,x+1=0,再解即可.
解答 解:(1)x(2x-5)=4x-10,
x(2x-5)=2(2x-5),
x(2x-5)-2(2x-5)=0,
(2x-5)(x-2)=0,
则2x-5=0,x-2=0,
故x1=2,x2=$\frac{5}{2}$;
(2)2x2-x-1=0,
(2x+1)(x-1)=0,
则2x+1=0,x-1=0,
故x1=-$\frac{1}{2}$ x2=1;
(3)x2+10x+9=0,
(x+9)(x+1)=0,
则x+9=0,x+1=0,
故x1=-9 x2=-1.
点评 此题主要考查了因式分解法解一元二次方程,因式分解法解一元二次方程的一般步骤:①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 已知反比例函数y=$\frac{6}{x}$在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB且AO=AB,则S△AOB=6.
已知反比例函数y=$\frac{6}{x}$在第一象限的图象如图所示,点A在其图象上,点B为x轴正半轴上一点,连接AO、AB且AO=AB,则S△AOB=6.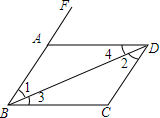 按图填空,并在横线内标明理由:
按图填空,并在横线内标明理由: 已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.
已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.