题目内容
4．（1）青岛国际帆船中心要修建一处公共服务设施，使它到三所运动员公寓A、B、C 的距离相等．若三所运动员公寓A、B、C的位置如图①所示，请你在图中确定这处公共服务设施（用点P表示）的位置；（不写作法，保留作图痕迹）（2）如图②，在10×10的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）．
①在图中作出△ABC关于直线l对称的△A1B1C1；（要求：A与A1，B与B1，C与C1相对应）
②若有一格点P到点A、B的距离相等（PA=PB），则网格中满足条件的点P共有9个．
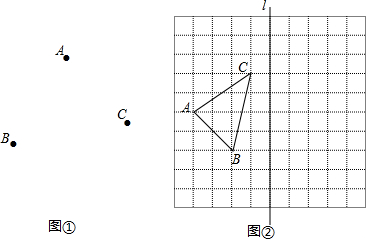
分析 （1）连接AB，AC，分别做出线段AB与AC的垂直平分线，交点即为所求的P点；
（2）①根据轴对称性质做出△ABC关于直线l对称的△A1B1C1即可；
②做出线段AB的垂直平分线，如图②的红线，即可确定出满足题意P的个数．
解答 
解：（1）如图①所示，点P为所求的点；
（2）①如图②所示，△A1B1C1为所求三角形；
②若有一格点P到点A、B的距离相等（PA=PB），如图②中的红线，
则网格中满足条件的点P共有9个，
故答案为：9
点评 此题考查了作图-应用与设计作图，作图-轴对称变换，熟练掌握线段垂直平分线定理是解本题的关键．
练习册系列答案
相关题目
已知：如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，DE⊥AB，垂足为点E，AE=BE．
9．
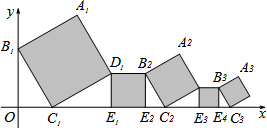已知在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点B1在y轴上，点C1，E1，E2，C2，E3，E4，C3在x轴上．若正方形A1B1C1D1的边长为2，∠B1C1O=60°，B1C1∥B2C2∥B3C3，则点A3到x轴的距离是（ ）
已知在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点B1在y轴上，点C1，E1，E2，C2，E3，E4，C3在x轴上．若正方形A1B1C1D1的边长为2，∠B1C1O=60°，B1C1∥B2C2∥B3C3，则点A3到x轴的距离是（ ）| A． | $\frac{1+\sqrt{3}}{9}$ | B． | $\frac{3+\sqrt{3}}{9}$ | C． | $\frac{3+\sqrt{3}}{3}$ | D． | $\frac{1+\sqrt{3}}{3}$ |
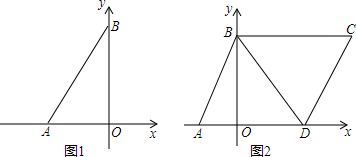
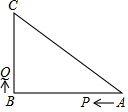如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm，P、Q是△ABC边上的两个动点，其 中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．