题目内容
1.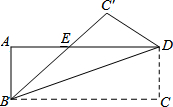 如图,长方形ABCD中,AB=4,BC=8,将长方形沿BC折叠,点C落在C′处.△BDE的面积是多少?
如图,长方形ABCD中,AB=4,BC=8,将长方形沿BC折叠,点C落在C′处.△BDE的面积是多少?
分析 由折叠可知,∠CBD=∠EBD,再由AD∥BC,得到∠CBD=∠EDB,即可得到∠EBD=∠EDB,于是得到BE=DE,设DE=x,则BE=x,AE=8-x,在Rt△ABE中,由勾股定理求出x的值,再由三角形的面积公式求出面积的值.
解答 解:由折叠可知,∠CBD=∠EBD,
∵AD∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE,
设DE=x,则BE=x,AE=8-x,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2即42+(8-x)2=x2,
解得:x=5,
所以S△BDE=$\frac{1}{2}$DE×AB=$\frac{1}{2}$×5×4=10.
点评 本题主要考查翻折变换的知识点,解答本题的关键是熟练掌握等腰三角形的判定与勾股定理的知识,此题难度不大.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
9.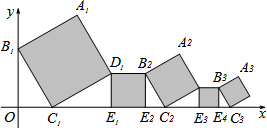 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )
已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )
 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )
已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )| A. | $\frac{1+\sqrt{3}}{9}$ | B. | $\frac{3+\sqrt{3}}{9}$ | C. | $\frac{3+\sqrt{3}}{3}$ | D. | $\frac{1+\sqrt{3}}{3}$ |
10.设6-$\sqrt{3}$的整数部分为a,小数部分为b,则a-$\frac{1}{b}$的值为( )
| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 2$+\sqrt{3}$ |
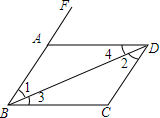 按图填空,并在横线内标明理由:
按图填空,并在横线内标明理由: 已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.
已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE. 请在图中作出△ABC的角平分线BD(要求保留作图痕迹).
请在图中作出△ABC的角平分线BD(要求保留作图痕迹).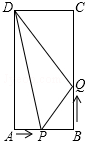 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.