题目内容
13.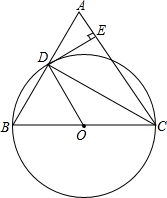 △ABC中,AB=AC,以BC为直径的⊙O与AB交于D,切线DE⊥AC于E,求证:AE=$\frac{1}{3}$CE.
△ABC中,AB=AC,以BC为直径的⊙O与AB交于D,切线DE⊥AC于E,求证:AE=$\frac{1}{3}$CE.
分析 由DE是⊙O的切线和BC为⊙O直径的,证明△ABC是等边三角形,然后根据直角三角形的性质证得结论.
解答 解:∵DE是⊙O的切线,
∴∠ODE=90°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DEC+∠EDC=∠ODC+∠CDE=90°,
∴∠ODC=∠DCE,
∵OD=OC,
∴∠OCD=∠ODC,
∵BC为⊙O直径的,
∴∠BDC=∠ADC=90°,
∴∠A=∠B,
∴AC=BC,∵AB=AC,
∴△ABC是等边三角形,
∴∠A=∠B=60°,
∴AD=BD=$\frac{1}{2}$AB,
在Rt△AED中,∠A=60°,
∴∠ADE=30°,
∴AE=$\frac{1}{2}$AD=$\frac{1}{4}$AC,CE=AC-AE=$\frac{3}{4}$AC,
∴$\frac{CE}{AE}$=3,
∴AE=$\frac{1}{3}$CE.
点评 本题考查了切线的性质,等边三角形的判定和性质,锐角三角函数,证明△ABC是等边三角形是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
7.今年4月,全国山地越野车大赛在我市某区举行,其中8名选手某项得分如表:
则这8名选手得分的众数、中位数分别是( )
| 得分 | 80 | 85 | 87 | 90 |
| 人数 | 1 | 3 | 2 | 2 |
| A. | 85、85 | B. | 87、85 | C. | 85、86 | D. | 85、87 |
4.下列正确的是( )
| A. | (π-3.14)0是无理数 | B. | $\sqrt{(-5)^{2}}=-5$ | C. | (x2)2=x5 | D. | $(-\frac{1}{4})^{-2}=16$ |
5. 如图,AD是正五边形ABCDE的一条对角线,则∠BAD=( )
如图,AD是正五边形ABCDE的一条对角线,则∠BAD=( )
 如图,AD是正五边形ABCDE的一条对角线,则∠BAD=( )
如图,AD是正五边形ABCDE的一条对角线,则∠BAD=( )| A. | 36° | B. | 70° | C. | 72° | D. | 108° |
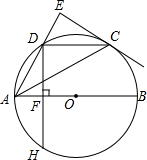 如图,AB是⊙O的直径.点C、D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF丄AB于点F,交⊙O于点H.连接DC、AC.
如图,AB是⊙O的直径.点C、D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF丄AB于点F,交⊙O于点H.连接DC、AC. 如图,已知△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,BD=AD,DE=DC,求证:BF⊥AC.
如图,已知△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,BD=AD,DE=DC,求证:BF⊥AC.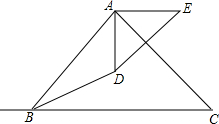 如图,已知AB⊥AC,DA⊥AE,AB=AC,AD=AE,求证:BD=CE.
如图,已知AB⊥AC,DA⊥AE,AB=AC,AD=AE,求证:BD=CE.