题目内容
5. 如图,AD是正五边形ABCDE的一条对角线,则∠BAD=( )
如图,AD是正五边形ABCDE的一条对角线,则∠BAD=( )| A. | 36° | B. | 70° | C. | 72° | D. | 108° |
分析 利用多边形内角和公式求得∠E的度数,在等腰三角形AED中可求得∠EAD的读数,进而求得∠BAD的度数.
解答 解:∵正五边形ABCDE的内角和为(5-2)×180°=540°,
∴∠E=$\frac{1}{5}$×540°=108°,∠BAE=108°
又∵EA=ED,
∴∠EAD=$\frac{1}{2}$×(180°-108°)=36°,
∴∠BAD=∠BAE-∠EAD=72°,
故选:C.
点评 本题考查了正多边形的计算,重点掌握正多边形内角和公式是关键.

练习册系列答案
相关题目
19.已知∠α=35°,则∠α的补角的度数是( )
| A. | 55° | B. | 65° | C. | 145° | D. | 165° |
16. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )| A. | 3:2 | B. | 3:1 | C. | 1:1 | D. | 1:2 |
10.八年2班组织了一次经典诵读比赛,甲、乙两组各10人的比赛成绩如下表(10 分制):
(I)甲组数据的中位数是9.5,乙组数据的众数是10;
(Ⅱ)计算乙组数据的平均数和方差;
(Ⅲ)已知甲组数据的方差是1.4分2,则成绩较为整齐的是乙组.
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(Ⅱ)计算乙组数据的平均数和方差;
(Ⅲ)已知甲组数据的方差是1.4分2,则成绩较为整齐的是乙组.
17.下列运算正确的是( )
| A. | a2+a3=a5 | B. | a6÷a2=a3 | C. | (-a2)3=a6 | D. | -2a•a2=-2a3 |
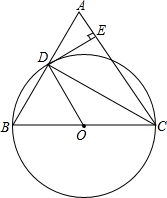 △ABC中,AB=AC,以BC为直径的⊙O与AB交于D,切线DE⊥AC于E,求证:AE=$\frac{1}{3}$CE.
△ABC中,AB=AC,以BC为直径的⊙O与AB交于D,切线DE⊥AC于E,求证:AE=$\frac{1}{3}$CE.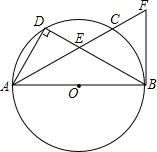 如图,AB是⊙O的直径,点C在⊙O上,点D是$\widehat{AC}$的中点,连接AD,BD.射线AC与BD相交于点E,与⊙O过点B的切线相交于点F,DE=4,BE=8.
如图,AB是⊙O的直径,点C在⊙O上,点D是$\widehat{AC}$的中点,连接AD,BD.射线AC与BD相交于点E,与⊙O过点B的切线相交于点F,DE=4,BE=8. 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使∠ABC不是直角三角形的概率是$\frac{3}{7}$.
如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使∠ABC不是直角三角形的概率是$\frac{3}{7}$.