题目内容
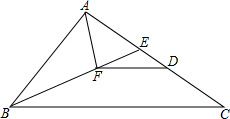 已知:如图,点E在△ABC的边AC上,且∠AEB=∠ABC.
已知:如图,点E在△ABC的边AC上,且∠AEB=∠ABC.(1)求证:∠ABE=∠C;
(2)若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=6,AC=10,求DC的长;
(3)若BE平分∠ABC,AF平分∠BAC,且FD∥BC交AC于点D,连接FC,则△DFC是什么三角形?为什么?
考点:全等三角形的判定与性质,平行线的性质
专题:
分析:(1)根据∠AEB=∠EBC+∠C、∠ABC=∠EBC+∠ABE和∠AEB=∠ABC,即可求得∠ABE=∠C;
(2)易证∠ADF=∠ABF和∠ADF=∠ABF,即可证明△BAF≌△DAF,可得AD=AB,即可解题;
(3)过点F分别作FH⊥AB,FN⊥BC,FM⊥AC,连接FC,易证FH=FN,和FH=FM,可得FM=FN,即可求得∠MCF=∠NCF,再根据∠DFC=∠BCF,即可求证△DFC是等腰三角形.
(2)易证∠ADF=∠ABF和∠ADF=∠ABF,即可证明△BAF≌△DAF,可得AD=AB,即可解题;
(3)过点F分别作FH⊥AB,FN⊥BC,FM⊥AC,连接FC,易证FH=FN,和FH=FM,可得FM=FN,即可求得∠MCF=∠NCF,再根据∠DFC=∠BCF,即可求证△DFC是等腰三角形.
解答:(1)证明:∵∠AEB=∠ABC,
且∠AEB=∠EBC+∠C,∠ABC=∠EBC+∠ABE,
∴∠EBC+∠C=∠EBC+∠ABE,
∴∠ABE=∠C;
(2)解:∵∠BAE的平分线AF交BE于F,
∴∠BAF=∠DAF,
∵FD∥BC交AC于D,
∴∠ADF=∠C,
∵∠ABE=∠C,
∴∠ADF=∠ABE,即∠ADF=∠ABF,
在△BAF和△DAF中,
,
∴△BAF≌△DAF(AAS),
∴AD=AB=6,
∴DC=AC-AD=10-6=4.
(3)解:△DFC是等腰三角形.
理由:过点F分别作FH⊥AB,FN⊥BC,FM⊥AC,连接FC,
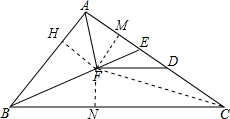
∵BF平分∠ABC,
∴FH=FN,
∵AF平分∠BAC,
∴FH=FM,
∴FM=FN,
∴∠MCF=∠NCF,
∵FD∥BC,
∴∠DFC=∠BCF,
∴∠DFC=∠MCF,
∴DF=DC,
∴△DFC是等腰三角形.
且∠AEB=∠EBC+∠C,∠ABC=∠EBC+∠ABE,
∴∠EBC+∠C=∠EBC+∠ABE,
∴∠ABE=∠C;
(2)解:∵∠BAE的平分线AF交BE于F,
∴∠BAF=∠DAF,
∵FD∥BC交AC于D,
∴∠ADF=∠C,
∵∠ABE=∠C,
∴∠ADF=∠ABE,即∠ADF=∠ABF,
在△BAF和△DAF中,
|
∴△BAF≌△DAF(AAS),
∴AD=AB=6,
∴DC=AC-AD=10-6=4.
(3)解:△DFC是等腰三角形.
理由:过点F分别作FH⊥AB,FN⊥BC,FM⊥AC,连接FC,

∵BF平分∠ABC,
∴FH=FN,
∵AF平分∠BAC,
∴FH=FM,
∴FM=FN,
∴∠MCF=∠NCF,
∵FD∥BC,
∴∠DFC=∠BCF,
∴∠DFC=∠MCF,
∴DF=DC,
∴△DFC是等腰三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BAF≌△DAF是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,DE∥BC,AD:AB=1:3,则△ADE与四边形BCED的面积比是
如图,DE∥BC,AD:AB=1:3,则△ADE与四边形BCED的面积比是 如图所示,在平面直角坐标系第二象限中,△ABO的顶点B在x轴上坐标为(-4,0),OA=6,且∠AOB=30°.
如图所示,在平面直角坐标系第二象限中,△ABO的顶点B在x轴上坐标为(-4,0),OA=6,且∠AOB=30°.