题目内容
 如图所示,在平面直角坐标系第二象限中,△ABO的顶点B在x轴上坐标为(-4,0),OA=6,且∠AOB=30°.
如图所示,在平面直角坐标系第二象限中,△ABO的顶点B在x轴上坐标为(-4,0),OA=6,且∠AOB=30°.(1)请作出△ABO绕点O顺时针旋转30°后形成的图形△A′B′O.
(2)连接AA′,BB′,求△AA′O的面积和四边形ABB′A′的面积.
(3)求连线AA′所在直线的函数解析式.
考点:作图-旋转变换,待定系数法求一次函数解析式
专题:
分析:(1)直接利用旋转的性质得出对应点坐标进而得出答案;
(2)首先求出旋转后三角形的高,进而分别得出两图形的面积;
(3)首先求出图形求出A,A′点坐标,进而利用待定系数法求一次函数解析式即可.
(2)首先求出旋转后三角形的高,进而分别得出两图形的面积;
(3)首先求出图形求出A,A′点坐标,进而利用待定系数法求一次函数解析式即可.
解答: 解:(1)如图所示:△A′B′O即为所求;
解:(1)如图所示:△A′B′O即为所求;
(2)过点A′C⊥AO与点C,过点B作BD⊥AO于点D,
∵△ABO绕点O顺时针旋转30°后形成的图形△A′B′O,
B在x轴上坐标为(-4,0),OA=6,且∠AOB=30°,
∴A′C=3,BD=2,
∴S△AOA′=
×A′C×AO=
×3×6=9,
S四边形ABB′A′=S△ABA′+S△ABB′=
×A′C×AB′+
×BD×AB′=
×(6-4)×(3+2)=5;
(3)过点A作AE⊥x轴于点E,过点A′作A′F⊥y轴于点F,
∵∠AOE=30°,∠AOA′=30°,
∴∠A′OF=30°,
∴AE=
AO=A′F=3,
FO=EO=3
,
故A(-3
,3),A′(-3,3
)
设直线AA′的解析式为:y=kx+b,
则
,
解得:
,
故AA′所在直线的函数解析式为:y=x+3+3
.
 解:(1)如图所示:△A′B′O即为所求;
解:(1)如图所示:△A′B′O即为所求;(2)过点A′C⊥AO与点C,过点B作BD⊥AO于点D,
∵△ABO绕点O顺时针旋转30°后形成的图形△A′B′O,
B在x轴上坐标为(-4,0),OA=6,且∠AOB=30°,
∴A′C=3,BD=2,
∴S△AOA′=
| 1 |
| 2 |
| 1 |
| 2 |
S四边形ABB′A′=S△ABA′+S△ABB′=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)过点A作AE⊥x轴于点E,过点A′作A′F⊥y轴于点F,
∵∠AOE=30°,∠AOA′=30°,
∴∠A′OF=30°,
∴AE=
| 1 |
| 2 |
FO=EO=3
| 3 |
故A(-3
| 3 |
| 3 |
设直线AA′的解析式为:y=kx+b,
则
|
解得:
|
故AA′所在直线的函数解析式为:y=x+3+3
| 3 |
点评:此题主要考查了待定系数法求一次函数解析式以及旋转变换等知识,得出对应点位置是解题关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
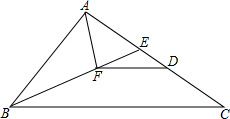 已知:如图,点E在△ABC的边AC上,且∠AEB=∠ABC.
已知:如图,点E在△ABC的边AC上,且∠AEB=∠ABC. 如图,已知AB为⊙O的弦,OD⊥AB于点C,DA与⊙O相切于点A,若AB=8cm,其弦心距等于3cm,则DA=
如图,已知AB为⊙O的弦,OD⊥AB于点C,DA与⊙O相切于点A,若AB=8cm,其弦心距等于3cm,则DA= 如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2.
如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2.