题目内容
已知△ABC的三边分别为a,b,c,且满足(a+2b-11)2+|2a-b-2|=10c-25-c2.请你判断△ABC的形状,并求出其中周长与面积.
考点:因式分解的应用,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:首先把原等式变形为(a+2b-11)2+|2a-b-2|+(c-5)2=0,利用非负数的性质,建立二元一次方程组,求得a、b、c的数值,利用勾股定理的逆定理判定三角形的形状,进一步求得周长和面积即可.
解答:解:∵(a+2b-11)2+|2a-b-2|=10c-25-c2,
∴(a+2b-11)2+|2a-b-2|+(c-5)2=0,
∴
,c-5=0,
∴a=3,b=4,c=5,
∵32+42=52,
∴△ABC为直角三角形,
∴△ABC的周长为3+4+5=12;
面积为
×3×4=6.
∴(a+2b-11)2+|2a-b-2|+(c-5)2=0,
∴
|
∴a=3,b=4,c=5,
∵32+42=52,
∴△ABC为直角三角形,
∴△ABC的周长为3+4+5=12;
面积为
| 1 |
| 2 |
点评:此题考查因式分解的运用,非负数的性质,解二元一次方程组,勾股定理逆定理以及三角形的周长和面积的计算方法;注意解题的思路与方法的灵活性.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
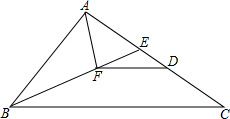 已知:如图,点E在△ABC的边AC上,且∠AEB=∠ABC.
已知:如图,点E在△ABC的边AC上,且∠AEB=∠ABC.