题目内容
15.已知关于x的不等式(m-1)x>6,两边同除以m-1,得x<$\frac{6}{m-1}$,试化简:|m-1|-|2-m|.分析 首先根据不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变,可得m-1<0,所以m<1;然后判断出2-m的正负,求出|m-1|-|2-m|的值是多少即可.
解答 解:因为(m-1)x>6,两边同除以m-1,得x<$\frac{6}{m-1}$,
所以m-1<0,m<1,
所以2-m>0,
所以|m-1|-|2-m|
=(1-m)-(2-m)
=1-m-2+m
=-1
点评 此题主要考查了不等式的基本性质:(1)不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;(2)不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;(3)等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变;解答此题的关键是判断出m-1<0.

练习册系列答案
相关题目
5.如图1,动点P从点B出发,以2厘米/秒的速度沿路径B-C-D-E-F-A运动,设运动时间为t(秒),当点P不与点A、B重合时,△ABP的面积S(平方厘米)关于时间t(秒)的函数图象2所示,若AB=6厘米,则下列结论正确的是( )
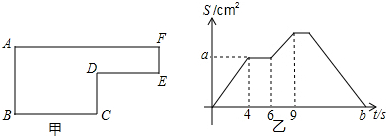

| A. | 图1中BC的长是4厘米 | B. | 图2中的a是12 | ||
| C. | 图1中的图形面积是60平方厘米 | D. | 图2中的b是19 |
3.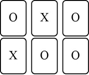 怡君手上有24张卡片,其中12张卡片被画上O记号,另外12张卡片被画上X记号.如图表示怡君从手上拿出6张卡片放在桌面的情形,且她打算从手上剩下的卡片中抽出一张卡片.若怡君手上剩下的每张卡片被抽出的机会相等,则她抽出O记号卡片的机率为何?( )
怡君手上有24张卡片,其中12张卡片被画上O记号,另外12张卡片被画上X记号.如图表示怡君从手上拿出6张卡片放在桌面的情形,且她打算从手上剩下的卡片中抽出一张卡片.若怡君手上剩下的每张卡片被抽出的机会相等,则她抽出O记号卡片的机率为何?( )
 怡君手上有24张卡片,其中12张卡片被画上O记号,另外12张卡片被画上X记号.如图表示怡君从手上拿出6张卡片放在桌面的情形,且她打算从手上剩下的卡片中抽出一张卡片.若怡君手上剩下的每张卡片被抽出的机会相等,则她抽出O记号卡片的机率为何?( )
怡君手上有24张卡片,其中12张卡片被画上O记号,另外12张卡片被画上X记号.如图表示怡君从手上拿出6张卡片放在桌面的情形,且她打算从手上剩下的卡片中抽出一张卡片.若怡君手上剩下的每张卡片被抽出的机会相等,则她抽出O记号卡片的机率为何?( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
 我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论. 如图,已知∠1+∠2=180°,DG∥AC,证明:∠A=∠DFE.
如图,已知∠1+∠2=180°,DG∥AC,证明:∠A=∠DFE.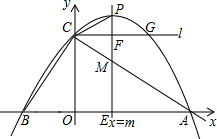 如图,直线y=2x+4与x轴、y轴相交于B、C两点,抛物线y=ax2-3ax+c过点B、C,且与x轴另一个交点为A,过点C作x轴的平行线l,交抛物线于点G.
如图,直线y=2x+4与x轴、y轴相交于B、C两点,抛物线y=ax2-3ax+c过点B、C,且与x轴另一个交点为A,过点C作x轴的平行线l,交抛物线于点G.