题目内容
3.已知抛物线y=$\frac{1}{4}$x2-1与x轴正半轴交于C点,顶点为D点.(1)求点C,D的坐标;
(2)如图1,过O点任作直线交抛物线于A、B,过B点作BE⊥x轴于E,求OB-BE的值;
(3)如图2,过P(0,-2)作直线交y轴右端的抛物线于M、N,若PM=PN,求直线MN的解析式.

分析 (1)令y=0,解方程可得点C坐标,利用配方法可得点D坐标.
(2)设B(m,$\frac{1}{4}$m2-1),求出OB、BE(用m的代数式表示)即可解决问题.
(3)如图2中,作ME⊥y轴于E,NF⊥y轴于F.由PM=MN,可以假设M(m,$\frac{1}{4}$m2-1),N(2m,m2-1),由ME∥NF,得到$\frac{ME}{NF}$=$\frac{PE}{PF}$=$\frac{1}{2}$,列出方程求出m,求出点M坐标,利用待定系数法即可解决问题.
解答 解:(1)对于抛物线y=$\frac{1}{4}$x2-1,令y=0,得$\frac{1}{4}$x2-1=0,解得x=±2,
∴点C坐标(2,0),抛物线顶点D坐标(0,-1).
(2)设B(m,$\frac{1}{4}$m2-1),
则OB=$\sqrt{{m}^{2}+(\frac{1}{4}{m}^{2}-1)^{2}}$=$\sqrt{\frac{1}{16}{m}^{4}+\frac{1}{2}{m}^{2}+1}$=$\frac{1}{4}$m2+1,
∵BE⊥x轴于E,
∴BE=$\frac{1}{4}$m2-1,
∴OB-BE=$\frac{1}{4}$m2+1-($\frac{1}{4}$m2-1)=2.
(3)如图2中,作ME⊥y轴于E,NF⊥y轴于F.
∵PM=MN,
∴可以假设M(m,$\frac{1}{4}$m2-1),N(2m,m2-1),
∵ME∥NF,
∴$\frac{ME}{NF}$=$\frac{PE}{PF}$=$\frac{1}{2}$,
∴$\frac{1+\frac{1}{4}{m}^{2}}{1+{m}^{2}}$=$\frac{1}{2}$,
∵m>0,
∴m=$\sqrt{2}$,
∴M($\sqrt{2}$,-$\frac{1}{2}$),
设直线MN的解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=-2}\\{\sqrt{2}k+b=-\frac{1}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3\sqrt{2}}{4}}\\{b=-2}\end{array}\right.$,
∴直线MN的解析式为y=$\frac{3\sqrt{2}}{4}$x-2.
点评 本题考查二次函数综合题、一次函数、勾股定理.平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,属于中考常考题型.



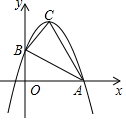 如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y铀的交点为B(0,3),其顶点为C,对称轴为x=1.
如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y铀的交点为B(0,3),其顶点为C,对称轴为x=1.