题目内容
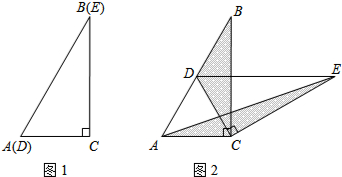
 如图,AE,AD分别是△ABC的高和角平分线,且∠B=30°,∠C=70°.
如图,AE,AD分别是△ABC的高和角平分线,且∠B=30°,∠C=70°.(1)求∠EAC的度数;
(2)求∠ADE的度数.(写明过程)
考点:三角形内角和定理
专题:
分析:(1)先根据AD⊥BC求出∠AEC的度数,再由三角形内角和定理即可得出结论;
(2)先根据三角形内角和定理求出∠BAC的度数,再根据AD是△ABC的角平分线求出∠BAD的度数,由三角形外角的性质即可得出结论.
(2)先根据三角形内角和定理求出∠BAC的度数,再根据AD是△ABC的角平分线求出∠BAD的度数,由三角形外角的性质即可得出结论.
解答:解:(1)∵AD⊥BC,
∴∠AEC=90°,
∵∠C=70°,
∴∠EAC=180°-90°-70°=20°;
(2)∵△ABC中,∠B=30°,∠C=70°
∴∠BAC=180°-30°-70°=80°.
∵AD是△ABC的角平分线,
∴∠BAD=
∠BAC=
×80°=40°,
∵∠ADE是△ABD的外角,
∴∠ADE=∠B+∠BAD=30°+40°=70°.
∴∠AEC=90°,
∵∠C=70°,
∴∠EAC=180°-90°-70°=20°;
(2)∵△ABC中,∠B=30°,∠C=70°
∴∠BAC=180°-30°-70°=80°.
∵AD是△ABC的角平分线,
∴∠BAD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ADE是△ABD的外角,
∴∠ADE=∠B+∠BAD=30°+40°=70°.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,AB是⊙O的直径,AC是弦,OD⊥AC于点E,交⊙O于点F,连接BF、CF,∠D=∠BFC.
如图,AB是⊙O的直径,AC是弦,OD⊥AC于点E,交⊙O于点F,连接BF、CF,∠D=∠BFC. 已知:如图,点E,F是?ABCD中AB,DC边上的点,且AE=CF,联结DE,BF.求证:DE=BF.
已知:如图,点E,F是?ABCD中AB,DC边上的点,且AE=CF,联结DE,BF.求证:DE=BF.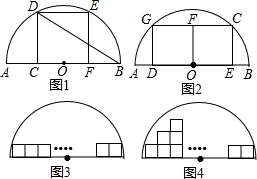 正方形和圆都是人们比较喜欢的图形,给人以美得感受.我校数学兴趣小组在研究性学习中发现:
正方形和圆都是人们比较喜欢的图形,给人以美得感受.我校数学兴趣小组在研究性学习中发现: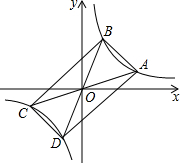 如图,在直角坐标系中,A,B,C,D四点在反比例函数y=
如图,在直角坐标系中,A,B,C,D四点在反比例函数y= 如图,在梯形ABCD中,AD∥BC,如果∠ABC=60°,BD平分∠ABC,且BD⊥DC,CD=4,那么梯形ABCD的周长是
如图,在梯形ABCD中,AD∥BC,如果∠ABC=60°,BD平分∠ABC,且BD⊥DC,CD=4,那么梯形ABCD的周长是