题目内容
5. 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′位置,AB′与CD交于点E,且AB=8,AD=4.
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′位置,AB′与CD交于点E,且AB=8,AD=4.(1)求证:AE=EC;
(2)求EC的长;
(3)点P为线段AC上任一点,PG⊥AE于G,PH⊥EC于H.求PG+PH的值,并说明理由.
分析 (1)由翻折变换的性质可知:∠EAC=∠BAC,由平行线的性质可知∠ECA=∠BAC,故∠EAC=∠ECA,从而得到EA=EC;
(2)设EA=EC=x,DE=8-x,然后在Rt△DEA中,由勾股定理列方程求解即可;
(3)根据S△AEP+S△ECP=S△ECA求解即可.
解答 解:(1)由翻折变换的性质可知:∠EAC=∠BAC,
∵DC∥AB,
∴∠ECA=∠BAC.
∴∠EAC=∠ECA.
∴EA=EC.
(2)设EA=EC=x,DE=8-x;
在Rt△DEA中,由勾股定理得:AE2=AD2+DE2,即x2=(8-x)2+42,
解得:x=5.
∴EC=5.
(3)如图所示;连接EP.
∵PG⊥AE于G,PH⊥EC于H,
∴${S}_{△AEP}=\frac{1}{2}AE•GP$,${S}_{△ECP}=\frac{1}{2}EC•PH$.
∵S△AEP+S△ECP=S△ECA,
∴$\frac{1}{2}AE•GP+\frac{1}{2}EC•PH$=$\frac{1}{2}EC•AD$,即$\frac{1}{2}×5×PG+\frac{1}{2}×5×PH$=$\frac{1}{2}×5×4$.
∴PG+PH=4.
点评 本题主要考查的是翻折的性质、勾股定理的应用、等腰三角形的判定,利用面积求得PG+PH=4是解题的关键.

练习册系列答案
相关题目
13.能把一个三角形分成两个面积相等的三角形是三角形的( )
| A. | 中线 | B. | 高线 | C. | 角平分线 | D. | 以上都不对 |
15.如果|a|=-a,则a的值不可能等于( )
| A. | 3 | B. | -3 | C. | 0 | D. | (-7)7 |
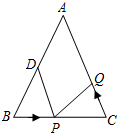 如图,已知△ABC中,AB=AC=10厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
如图,已知△ABC中,AB=AC=10厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动. (1)请在所给方格纸(由边长为1的小正方形无缝隙不重叠的拼接而成)上,作一个三角形,使它的三个顶点的坐标为(1,0),(3,1),(2,4);并求出该三角形的面积.
(1)请在所给方格纸(由边长为1的小正方形无缝隙不重叠的拼接而成)上,作一个三角形,使它的三个顶点的坐标为(1,0),(3,1),(2,4);并求出该三角形的面积.